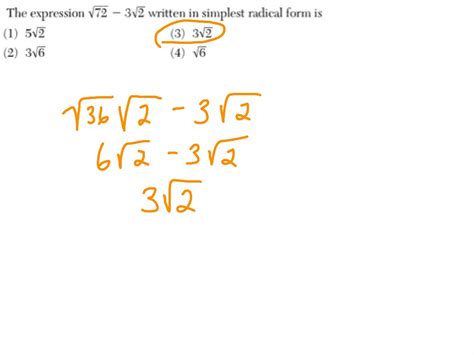Simplifying Math: Understanding Reduced Radical Form

Quick Links :

Mathematics is an essential part of our daily lives, and yet, many people find it challenging, especially when it comes to complex mathematical concepts. One such concept is radicals, which can be daunting for students and professionals alike. However, understanding reduced radical form can make a significant difference in simplifying math problems.

In this article, we will delve into the world of radicals, explore what reduced radical form is, and discuss its importance in mathematics. We will also provide examples and explanations to help you grasp this concept and simplify math problems.

What are Radicals?

Radicals are mathematical expressions that contain a root, such as square roots, cube roots, or nth roots. They are used to represent the operation of finding the root of a number or expression. For instance, the square root of a number is a value that, when multiplied by itself, gives the original number.

Radicals are essential in mathematics, particularly in algebra, geometry, and calculus. They help solve equations, simplify expressions, and model real-world problems. However, radicals can be complex and challenging to work with, which is where reduced radical form comes in.

What is Reduced Radical Form?

Reduced radical form is a way of expressing radicals in a simplified manner. It involves finding the largest perfect square or perfect cube that divides the radicand (the number or expression inside the radical) and rewriting the radical in a simpler form.

For example, the radical √16 can be simplified to 4, as 4 multiplied by 4 equals 16. Similarly, the radical √48 can be simplified to 4√3, as 48 can be divided by 16 (the largest perfect square that divides 48), and the result is 3.

Reduced radical form is crucial in mathematics because it helps simplify complex expressions, making it easier to work with them. It also enables us to perform operations, such as addition and subtraction, on radicals.

Why is Reduced Radical Form Important?

Reduced radical form is essential in mathematics for several reasons:

• Simplifies complex expressions: Reduced radical form helps simplify complex expressions, making it easier to work with them.
• Enables operations: Reduced radical form enables us to perform operations, such as addition and subtraction, on radicals.
• Improves problem-solving: Reduced radical form improves problem-solving skills, as it allows us to simplify expressions and equations.
• Enhances understanding: Reduced radical form enhances our understanding of mathematical concepts, such as algebra and geometry.

How to Simplify Radicals to Reduced Radical Form

Simplifying radicals to reduced radical form involves several steps:

1. Find the largest perfect square or perfect cube: Find the largest perfect square or perfect cube that divides the radicand.
2. Divide the radicand: Divide the radicand by the perfect square or perfect cube.
3. Rewrite the radical: Rewrite the radical in a simpler form using the result from step 2.

For example, to simplify the radical √48, we follow these steps:

1. Find the largest perfect square that divides 48, which is 16.
2. Divide 48 by 16, resulting in 3.
3. Rewrite the radical as 4√3.

Example 1: Simplifying √16

To simplify the radical √16, we follow these steps:

1. Find the largest perfect square that divides 16, which is 16.
2. Divide 16 by 16, resulting in 1.
3. Rewrite the radical as 4.

Example 2: Simplifying √48

To simplify the radical √48, we follow these steps:

1. Find the largest perfect square that divides 48, which is 16.
2. Divide 48 by 16, resulting in 3.
3. Rewrite the radical as 4√3.

Common Mistakes to Avoid

When simplifying radicals to reduced radical form, there are several common mistakes to avoid:

• Not finding the largest perfect square or perfect cube: Failing to find the largest perfect square or perfect cube that divides the radicand can result in an incorrect simplification.
• Not dividing the radicand correctly: Failing to divide the radicand correctly can result in an incorrect simplification.
• Not rewriting the radical correctly: Failing to rewrite the radical correctly can result in an incorrect simplification.

Conclusion

Reduced radical form is a crucial concept in mathematics that helps simplify complex expressions and enables us to perform operations on radicals. By understanding reduced radical form, we can improve our problem-solving skills and enhance our understanding of mathematical concepts. Remember to find the largest perfect square or perfect cube, divide the radicand correctly, and rewrite the radical correctly to simplify radicals to reduced radical form.

Now, it's your turn! Share your thoughts on reduced radical form in the comments below. Do you have any questions or examples you'd like to discuss? Let's start a conversation!