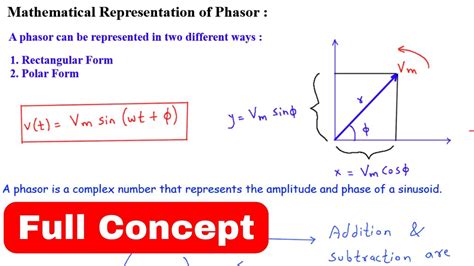
In electrical engineering, phasors are a fundamental concept used to represent AC circuits in a simplified manner. However, there are situations where it's necessary to convert phasor form to rectangular form. This conversion is essential in various applications, including filter design, circuit analysis, and signal processing. In this article, we'll explore three ways to convert phasor form to rectangular form.

Understanding Phasor Form
Before diving into the conversion methods, let's quickly review the phasor form. A phasor is a complex number that represents a sinusoidal signal in a compact form. It's expressed as:
A ∠ θ = A (cos θ + j sin θ)
where A is the amplitude, θ is the phase angle, and j is the imaginary unit.
Rectangular Form
The rectangular form, on the other hand, represents a complex number as a sum of real and imaginary parts:
a + jb
where a is the real part and b is the imaginary part.
Method 1: Using Euler's Formula
One way to convert phasor form to rectangular form is by using Euler's formula:
e^(jθ) = cos θ + j sin θ
We can multiply the amplitude A by Euler's formula to get:
A ∠ θ = A (cos θ + j sin θ) = A e^(jθ)
Now, we can expand the exponential term using the Euler's formula:
A ∠ θ = A (cos θ + j sin θ) = A cos θ + j A sin θ
This is the rectangular form of the phasor.

Method 2: Using the Cartesian Coordinate System
Another way to convert phasor form to rectangular form is by using the Cartesian coordinate system. Imagine a complex plane with the real axis (x-axis) and the imaginary axis (y-axis). We can plot the phasor on this plane using its amplitude and phase angle.
The x-coordinate of the phasor is given by:
a = A cos θ
The y-coordinate of the phasor is given by:
b = A sin θ
The rectangular form is then:
a + jb = A cos θ + j A sin θ

Method 3: Using the Phasor-to-Rectangular Conversion Formula
The third method is a straightforward formula-based approach. Given a phasor in the form:
A ∠ θ
We can convert it to rectangular form using the following formula:
a + jb = A cos θ + j A sin θ
This formula is derived from the Euler's formula and the Cartesian coordinate system.

Conclusion
Converting phasor form to rectangular form is an essential skill in electrical engineering and circuit analysis. We've explored three methods to achieve this conversion: using Euler's formula, the Cartesian coordinate system, and the phasor-to-rectangular conversion formula. By mastering these methods, you'll be able to work with phasors and rectangular forms with confidence.
Share Your Thoughts
Have you used any of these methods in your projects or studies? Do you have any questions or need further clarification? Share your thoughts in the comments below!
FAQ Section
What is the purpose of converting phasor form to rectangular form?
+Converting phasor form to rectangular form is necessary in various applications, including filter design, circuit analysis, and signal processing. It allows us to work with complex numbers in a more convenient and simplified manner.
Which method is the most straightforward way to convert phasor form to rectangular form?
+The phasor-to-rectangular conversion formula is the most straightforward method. It involves a simple calculation using the amplitude and phase angle of the phasor.
Can I use these methods to convert rectangular form to phasor form?
+No, these methods are specifically designed for converting phasor form to rectangular form. To convert rectangular form to phasor form, you'll need to use different methods, such as finding the amplitude and phase angle from the real and imaginary parts.