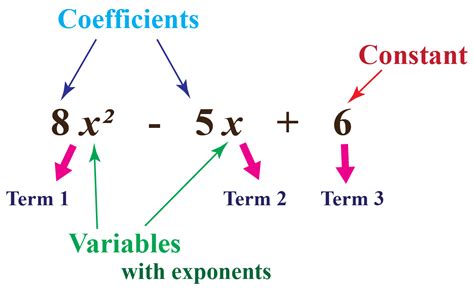
In mathematics, polynomials are one of the most fundamental concepts, and understanding their standard form is essential for working with them effectively. In this article, we will delve into the world of polynomials, explore what they are, and explain the significance of their standard form.
A polynomial is an algebraic expression consisting of variables, coefficients, and mathematical operations. It is a sum of terms, where each term is a product of a coefficient and one or more variables raised to a non-negative integer power. Polynomials can be written in various forms, but the standard form is a specific way of representing them that makes it easier to work with them.
Definition of a Polynomial in Standard Form
A polynomial in standard form is written in the following way:
ax^n + bx^(n-1) + cx^(n-2) + … + k
where:
- a, b, c, …, k are coefficients (numbers)
- x is the variable
- n is the degree of the polynomial (the highest power of the variable)
- The coefficients are written in decreasing order of the exponent of the variable
For example, the polynomial 3x^2 + 2x - 4 is in standard form because the coefficients are written in decreasing order of the exponent of the variable x.

Importance of Standard Form
Writing polynomials in standard form is crucial for several reasons:
- Easier comparison: When polynomials are in standard form, it is easier to compare them and determine if they are equal or not.
- Simplification: Standard form makes it easier to simplify polynomials by combining like terms.
- Addition and subtraction: When adding or subtracting polynomials, it is essential to have them in standard form to ensure that the correct terms are combined.
- Multiplication and division: Standard form is also necessary for multiplying and dividing polynomials.
How to Write a Polynomial in Standard Form
To write a polynomial in standard form, follow these steps:
- Write the terms in decreasing order of the exponent: Start with the term that has the highest exponent and end with the term that has the lowest exponent.
- Combine like terms: If there are any like terms (terms with the same variable and exponent), combine them by adding or subtracting their coefficients.
- Simplify the coefficients: Simplify the coefficients by performing any necessary arithmetic operations.
For example, consider the polynomial x^2 + 3x - 2x + 4. To write it in standard form, we need to combine the like terms:
x^2 + 3x - 2x + 4 = x^2 + x + 4
Now the polynomial is in standard form.
Examples of Polynomials in Standard Form
- 2x^3 + 3x^2 - 4x + 1
- x^4 - 2x^3 + 3x^2 + x - 1
- 3x^2 + 2x - 4
In each of these examples, the coefficients are written in decreasing order of the exponent of the variable x.
Conclusion
In conclusion, writing polynomials in standard form is an essential skill in mathematics. It allows us to work with polynomials more efficiently and makes it easier to compare, simplify, add, subtract, multiply, and divide them. By following the simple steps outlined above, you can ensure that your polynomials are always in standard form.
We hope this article has helped you understand the importance of standard form in polynomials. Do you have any questions or would you like to share your thoughts on this topic? Please feel free to comment below.
What is a polynomial?
+A polynomial is an algebraic expression consisting of variables, coefficients, and mathematical operations. It is a sum of terms, where each term is a product of a coefficient and one or more variables raised to a non-negative integer power.
Why is standard form important?
+Standard form is important because it makes it easier to compare, simplify, add, subtract, multiply, and divide polynomials. It also allows us to work with polynomials more efficiently.
How do I write a polynomial in standard form?
+To write a polynomial in standard form, write the terms in decreasing order of the exponent, combine like terms, and simplify the coefficients.