Graphing Quadratic In Standard Form Made Easy

Quick Links :

The world of quadratic equations! While they may seem daunting at first, graphing quadratic equations in standard form can be a breeze with the right approach. In this article, we'll delve into the realm of quadratic equations, exploring what they are, their importance, and most importantly, how to graph them with ease.

Quadratic equations are a fundamental concept in algebra and are used to model a wide range of real-world phenomena, from the trajectory of projectiles to the growth of populations. They are essential in various fields, including physics, engineering, economics, and computer science. Understanding how to graph quadratic equations is crucial for solving problems and making informed decisions in these fields.

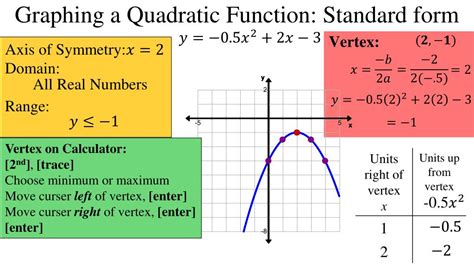
So, what exactly is a quadratic equation in standard form? A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two. The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. The graph of a quadratic equation is a parabola, which is a U-shaped curve that opens upwards or downwards.

Understanding the Components of a Quadratic Equation

To graph a quadratic equation, it's essential to understand the role of each component. The coefficient "a" determines the direction and width of the parabola. If a is positive, the parabola opens upwards; if a is negative, it opens downwards. The coefficient "b" determines the position of the vertex, which is the lowest or highest point on the parabola. The constant term "c" determines the y-intercept, which is the point where the parabola crosses the y-axis.

The Role of the Coefficient "a"

The coefficient "a" is a critical component of a quadratic equation. It determines the direction and width of the parabola. If a is positive, the parabola opens upwards, and if a is negative, it opens downwards. The value of a also affects the width of the parabola. If a is large, the parabola is narrower; if a is small, the parabola is wider.

The Role of the Coefficient "b"

The coefficient "b" determines the position of the vertex, which is the lowest or highest point on the parabola. The vertex is also the turning point of the parabola. If b is positive, the vertex is shifted to the right; if b is negative, the vertex is shifted to the left.

The Role of the Constant Term "c"

The constant term "c" determines the y-intercept, which is the point where the parabola crosses the y-axis. The value of c also affects the position of the vertex. If c is positive, the vertex is shifted upwards; if c is negative, the vertex is shifted downwards.

Graphing Quadratic Equations in Standard Form

Now that we've explored the components of a quadratic equation, let's dive into graphing them. Graphing a quadratic equation involves finding the vertex, axis of symmetry, and x-intercepts.

1. Find the Vertex: The vertex is the lowest or highest point on the parabola. To find the vertex, use the formula x = -b / 2a.
2. Find the Axis of Symmetry: The axis of symmetry is the vertical line that passes through the vertex. To find the axis of symmetry, use the formula x = -b / 2a.
3. Find the X-Intercepts: The x-intercepts are the points where the parabola crosses the x-axis. To find the x-intercepts, set y = 0 and solve for x.

Step-by-Step Example

Let's graph the quadratic equation x^2 + 4x + 4 = 0.

1. Find the Vertex: x = -4 / 2(1) = -2
2. Find the Axis of Symmetry: x = -4 / 2(1) = -2
3. Find the X-Intercepts: x^2 + 4x + 4 = 0 --> (x + 2)(x + 2) = 0 --> x + 2 = 0 --> x = -2

The vertex is (-2, 0), the axis of symmetry is x = -2, and the x-intercept is (-2, 0).

Tips and Tricks for Graphing Quadratic Equations

Here are some tips and tricks for graphing quadratic equations:

• Use the Formula: Use the formula x = -b / 2a to find the vertex and axis of symmetry.
• Use the Intercept Method: Use the intercept method to find the x-intercepts.
• Check Your Work: Check your work by plugging in values to ensure the graph is accurate.
• Use Graphing Tools: Use graphing tools, such as graphing calculators or software, to visualize the graph.

Conclusion

Graphing quadratic equations in standard form may seem daunting, but with the right approach, it can be a breeze. By understanding the components of a quadratic equation and using the step-by-step method, you can graph quadratic equations with ease. Remember to use the formula, intercept method, and graphing tools to ensure accuracy. With practice, you'll become a pro at graphing quadratic equations in no time!

We hope this article has been informative and helpful in your journey to master graphing quadratic equations. If you have any questions or comments, please feel free to share them below.