5 Ways To Express Equations In Logarithmic Form

Quick Links :

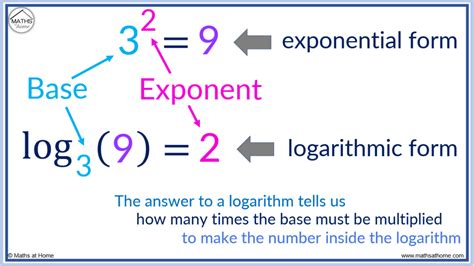
Logarithmic equations are a fundamental concept in mathematics, particularly in algebra and calculus. They have numerous applications in various fields, including physics, engineering, and finance. Understanding how to express equations in logarithmic form is essential for solving problems involving exponential growth or decay, pH levels, and statistical analysis, among others. In this article, we will explore five ways to express equations in logarithmic form.

Understanding Logarithmic Equations

A logarithmic equation is an equation in which the variable appears in the argument of a logarithmic function. In other words, it is an equation where the variable is inside a logarithm. Logarithmic equations can be used to model real-world phenomena, such as population growth, chemical reactions, and electrical circuits.

Why Express Equations in Logarithmic Form?

Expressing equations in logarithmic form can simplify complex problems and provide insights into the underlying relationships between variables. Logarithmic equations can:

• Reduce the complexity of exponential equations
• Reveal hidden patterns and relationships between variables
• Facilitate the solution of equations involving exponential growth or decay
• Enable the analysis of complex systems and phenomena

Method 1: Using Logarithmic Properties

One way to express equations in logarithmic form is to use the properties of logarithms. The three main logarithmic properties are:

• The product rule: log(ab) = log(a) + log(b)
• The quotient rule: log(a/b) = log(a) - log(b)
• The power rule: log(a^b) = b log(a)

By applying these properties, we can rewrite equations in logarithmic form.

Example: Express the equation 2^x = 10 in logarithmic form.

Using the power rule, we can rewrite the equation as x log(2) = log(10).

Method 2: Using Logarithmic Identities

Logarithmic identities are equations that involve logarithms and are true for all values of the variable. One common logarithmic identity is:

log(a) + log(b) = log(ab)

By using this identity, we can rewrite equations in logarithmic form.

Example: Express the equation log(x) + log(y) = log(10) in exponential form.

Using the logarithmic identity, we can rewrite the equation as log(xy) = log(10).

Method 3: Using Exponential Form

Exponential form is a way of expressing equations using exponents. To express an equation in logarithmic form, we can start with the exponential form and use the definition of a logarithm.

Example: Express the equation 10^x = 2 in logarithmic form.

Using the definition of a logarithm, we can rewrite the equation as x = log(2)/log(10).

Method 4: Using Algebraic Manipulation

Algebraic manipulation involves using algebraic techniques to rewrite equations in logarithmic form. One common technique is to use substitution.

Example: Express the equation 2^x + 3^x = 10 in logarithmic form.

By substituting u = 2^x and v = 3^x, we can rewrite the equation as u + v = 10.

Using the logarithmic properties, we can rewrite the equation as log(u) + log(v) = log(10).

Method 5: Using Graphical Analysis

Graphical analysis involves using graphs to analyze and solve equations. By plotting the graph of an equation, we can identify patterns and relationships between variables.

Example: Express the equation y = 2^x in logarithmic form.

By plotting the graph of the equation, we can see that it is an exponential curve. Using the definition of a logarithm, we can rewrite the equation as x = log(y)/log(2).

In conclusion, there are several ways to express equations in logarithmic form, including using logarithmic properties, identities, exponential form, algebraic manipulation, and graphical analysis. By mastering these techniques, we can simplify complex problems and gain insights into the underlying relationships between variables.

If you have any questions or need further clarification on any of the methods discussed in this article, please don't hesitate to ask in the comments section below. Share this article with your friends and colleagues who may be interested in learning more about logarithmic equations.