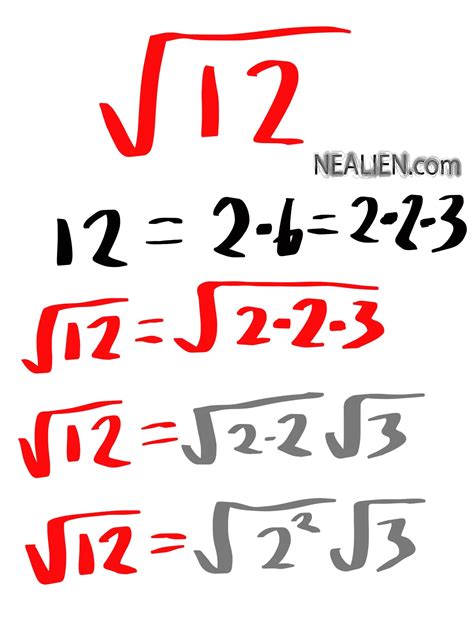Find The Square Root Of 12 In Radical Form Easily

Quick Links :

Finding the square root of a number can be a daunting task, especially when dealing with non-perfect squares. However, with the right approach and techniques, it can be made easier. In this article, we will explore how to find the square root of 12 in radical form easily.

Understanding Square Roots

Before diving into finding the square root of 12, it's essential to understand what a square root is. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16.

Perfect Squares vs. Non-Perfect Squares

Perfect squares are numbers that can be expressed as the square of an integer. For instance, 16 is a perfect square because it can be expressed as 4^2. On the other hand, non-perfect squares are numbers that cannot be expressed as the square of an integer. 12 is an example of a non-perfect square.

Methods for Finding Square Roots

There are several methods for finding square roots, including:

• Long Division Method: This method involves dividing the number by a series of perfect squares to find the square root.
• Factorization Method: This method involves factoring the number into its prime factors and then finding the square root of each factor.
• Radical Form Method: This method involves expressing the number in radical form, which is the most common method used for finding square roots of non-perfect squares.

Using the Radical Form Method

The radical form method involves expressing the number as a product of a perfect square and a non-perfect square. For example, to find the square root of 12, we can express it as:

√12 = √(4 × 3)

Since 4 is a perfect square, we can simplify the expression to:

√12 = 2√3

Finding the Square Root of 12

Using the radical form method, we can easily find the square root of 12. We can express 12 as:

12 = 4 × 3

Since 4 is a perfect square, we can simplify the expression to:

√12 = √(4 × 3) = 2√3

Therefore, the square root of 12 in radical form is 2√3.

Verifying the Answer

To verify our answer, we can square 2√3 to see if it equals 12:

(2√3)^2 = 4 × 3 = 12

As expected, the result equals 12, confirming that our answer is correct.

Conclusion

Finding the square root of 12 in radical form is a straightforward process that involves expressing the number as a product of a perfect square and a non-perfect square. By using the radical form method, we can easily simplify the expression and find the square root of 12 as 2√3.

Final Thoughts

In conclusion, finding square roots can be a challenging task, but with the right approach and techniques, it can be made easier. By understanding the different methods for finding square roots and using the radical form method, we can easily find the square root of non-perfect squares like 12.

Now, it's your turn! Try finding the square root of other non-perfect squares using the radical form method. Share your answers and any questions you may have in the comments below.