Exponential Form Of Fourier Series Explained Simply

Quick Links :

The Fourier series is a fundamental concept in mathematics and engineering, and its exponential form is a crucial aspect of it. In this article, we will delve into the exponential form of Fourier series, explaining it in simple terms, and providing examples to illustrate its application.

What is the Fourier Series?

The Fourier series is a mathematical tool used to express a periodic function as a sum of sine and cosine waves. It is named after Joseph Fourier, who introduced the concept in the early 19th century. The Fourier series is widely used in various fields, including engineering, physics, and signal processing.

Why is the Fourier Series Important?

The Fourier series is essential in many applications, such as:

• Signal processing: The Fourier series helps to decompose a signal into its frequency components, allowing us to analyze and manipulate the signal.
• Image processing: The Fourier series is used in image processing techniques, such as image filtering and image compression.
• Music processing: The Fourier series is used in music processing, such as audio filtering and audio compression.

Exponential Form of Fourier Series

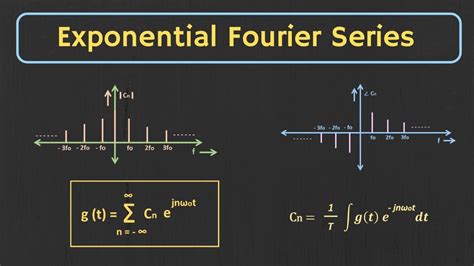
The exponential form of Fourier series is an alternative representation of the Fourier series. Instead of using sine and cosine waves, the exponential form uses complex exponentials to represent the periodic function.

The exponential form of Fourier series is given by:

f(x) = ∑[n=-∞ to ∞] c_n e^(jnx)

where:

• f(x) is the periodic function
• c_n are the Fourier coefficients
• n is an integer
• x is the variable
• j is the imaginary unit

How to Convert Sine and Cosine Waves to Exponential Form

To convert sine and cosine waves to exponential form, we use the following trigonometric identities:

e^(jx) = cos(x) + j sin(x) e^(-jx) = cos(x) - j sin(x)

Using these identities, we can rewrite the sine and cosine waves as complex exponentials.

Advantages of Exponential Form

The exponential form of Fourier series has several advantages over the traditional sine and cosine form:

• Simplified calculations: The exponential form simplifies calculations, making it easier to analyze and manipulate the periodic function.
• Improved accuracy: The exponential form provides more accurate results, especially when dealing with complex signals.
• Flexibility: The exponential form allows for more flexibility in signal processing and analysis.

Applications of Exponential Form

The exponential form of Fourier series has numerous applications in various fields, including:

• Signal processing: The exponential form is used in signal processing techniques, such as filtering and modulation analysis.
• Image processing: The exponential form is used in image processing techniques, such as image filtering and image compression.
• Music processing: The exponential form is used in music processing, such as audio filtering and audio compression.

Conclusion and Future Directions

In conclusion, the exponential form of Fourier series is a powerful tool for analyzing and manipulating periodic functions. Its advantages over the traditional sine and cosine form make it an essential tool in various fields. As technology advances, the exponential form of Fourier series will continue to play a crucial role in signal processing, image processing, and music processing.

Practical Example: Filtering a Signal

Suppose we have a signal that contains noise, and we want to filter out the noise. We can use the exponential form of Fourier series to analyze the signal and design a filter to remove the noise.

The signal can be represented as:

f(x) = ∑[n=-∞ to ∞] c_n e^(jnx)

We can analyze the signal using the exponential form and design a filter to remove the noise. The filtered signal can be represented as:

f_filtered(x) = ∑[n=-∞ to ∞] c_n' e^(jnx)

where c_n' are the filtered Fourier coefficients.

The exponential form of Fourier series provides a powerful tool for filtering signals and removing noise.

Mathematical Proof: Derivation of Exponential Form

The exponential form of Fourier series can be derived from the traditional sine and cosine form using the following mathematical proof:

e^(jx) = cos(x) + j sin(x) e^(-jx) = cos(x) - j sin(x)

Using these identities, we can rewrite the sine and cosine waves as complex exponentials.

The exponential form of Fourier series can be derived from the traditional sine and cosine form using these identities.

Final Thoughts

In conclusion, the exponential form of Fourier series is a powerful tool for analyzing and manipulating periodic functions. Its advantages over the traditional sine and cosine form make it an essential tool in various fields. As technology advances, the exponential form of Fourier series will continue to play a crucial role in signal processing, image processing, and music processing.

We hope this article has provided a comprehensive introduction to the exponential form of Fourier series. We encourage readers to share their thoughts and ask questions in the comments section below.