5 Ways To Convert Fractions To Radical Form

Quick Links :

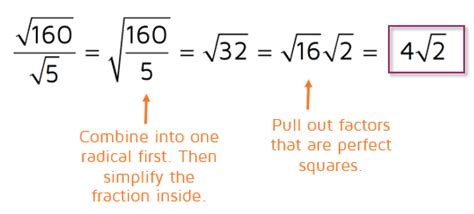
Converting fractions to radical form is an essential skill in mathematics, particularly in algebra and geometry. It allows us to simplify complex expressions and solve equations more efficiently. In this article, we will explore five ways to convert fractions to radical form, along with examples, explanations, and tips to help you master this skill.

Understanding Fractions and Radicals

Before we dive into the conversion methods, it's essential to understand the basics of fractions and radicals. A fraction is a way of expressing a part of a whole, with a numerator (top number) and a denominator (bottom number). For example, 3/4 is a fraction where 3 is the numerator and 4 is the denominator.

A radical, on the other hand, is a symbol used to represent the nth root of a number. For example, √16 is a radical expression that represents the square root of 16. In this article, we will focus on converting fractions to radical form, specifically using square roots, cube roots, and fourth roots.

Method 1: Simplifying Fractions Before Conversion

The first method involves simplifying the fraction before converting it to radical form. This step is crucial to ensure that the resulting radical expression is in its simplest form.

For example, let's convert the fraction 6/8 to radical form. To simplify the fraction, we can divide both the numerator and denominator by 2, resulting in 3/4. Now, we can convert the simplified fraction to radical form by taking the square root of the numerator and denominator separately:

3/4 = √(3²)/√(4²) = √9/√16 = 3/4

As you can see, the resulting radical expression is already in its simplest form.

Method 2: Using the Square Root Method

The second method involves using the square root method to convert fractions to radical form. This method is suitable for fractions with a denominator that is a perfect square.

For example, let's convert the fraction 5/9 to radical form using the square root method:

5/9 = √(5²)/√(9²) = √25/√81

Since 25 is not a perfect square, we can simplify the expression by taking the square root of 25:

√25 = √(5²) = 5

So, the resulting radical expression is:

5/√81

Method 3: Using the Cube Root Method

The third method involves using the cube root method to convert fractions to radical form. This method is suitable for fractions with a denominator that is a perfect cube.

For example, let's convert the fraction 2/27 to radical form using the cube root method:

2/27 = ∛(2³)/∛(27³) = ∛8/∛729

Since 8 is not a perfect cube, we can simplify the expression by taking the cube root of 8:

∛8 = ∛(2³) = 2

So, the resulting radical expression is:

2/∛729

Method 4: Using the Fourth Root Method

The fourth method involves using the fourth root method to convert fractions to radical form. This method is suitable for fractions with a denominator that is a perfect fourth power.

For example, let's convert the fraction 3/16 to radical form using the fourth root method:

3/16 = √/√ = √[4]81/√[4]65536

Since 81 is not a perfect fourth power, we can simplify the expression by taking the fourth root of 81:

√ = 3

So, the resulting radical expression is:

3/√[4]65536

Method 5: Using Rational Exponents

The fifth method involves using rational exponents to convert fractions to radical form. This method is suitable for fractions with a denominator that is a perfect power.

For example, let's convert the fraction 4/25 to radical form using rational exponents:

4/25 = 4 × 25^(-1) = 4 × (5^2)^(-1) = 4/5^2 = 4/√(5^4)

Since 5^4 is a perfect fourth power, we can simplify the expression by taking the fourth root of 5^4:

√(5^4) = 5

So, the resulting radical expression is:

4/5

Now that you've learned the five ways to convert fractions to radical form, it's time to practice and apply these methods to different types of fractions. Remember to simplify the fraction before conversion, and use the square root, cube root, fourth root, or rational exponent method depending on the denominator.

If you have any questions or need further clarification on any of the methods, please don't hesitate to ask in the comments section below. Share this article with your friends and classmates who may benefit from learning these essential math skills.