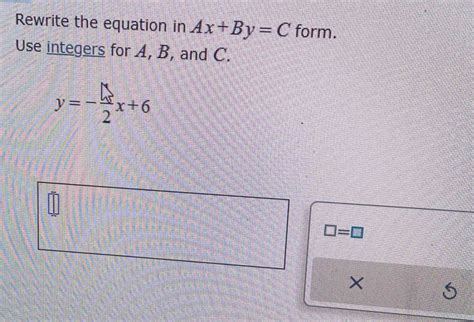
Equations are a fundamental part of mathematics, and being able to rewrite them in different forms is an essential skill. One of the most common forms of a linear equation is the Ax+By=C form, also known as the standard form. In this article, we will explore five ways to rewrite equations in Ax+By=C form.

Method 1: Rearranging Terms
One of the simplest ways to rewrite an equation in Ax+By=C form is to rearrange the terms. This involves moving all the x terms to one side of the equation and all the y terms to the other side.
For example, consider the equation 2x + 5 = 3y - 2. To rewrite this equation in Ax+By=C form, we need to move the 5 to the other side of the equation and combine like terms.
2x - 3y = -2 - 5 2x - 3y = -7
As you can see, the equation is now in Ax+By=C form, where A = 2, B = -3, and C = -7.
Method 2: Adding or Subtracting the Same Value
Another way to rewrite an equation in Ax+By=C form is to add or subtract the same value from both sides of the equation. This method is useful when the equation has a constant term on one side.
Consider the equation x - 2y = 4 + 2x. To rewrite this equation in Ax+By=C form, we need to subtract 2x from both sides of the equation.
x - 2x - 2y = 4 -x - 2y = 4
As you can see, the equation is now in Ax+By=C form, where A = -1, B = -2, and C = 4.

Method 3: Multiplying or Dividing by a Constant
Sometimes, we need to multiply or divide both sides of the equation by a constant to rewrite it in Ax+By=C form. This method is useful when the equation has coefficients that are not integers.
Consider the equation 0.5x + 2y = 3. To rewrite this equation in Ax+By=C form, we need to multiply both sides of the equation by 2.
0.5x * 2 + 2y * 2 = 3 * 2 x + 4y = 6
As you can see, the equation is now in Ax+By=C form, where A = 1, B = 4, and C = 6.
Method 4: Factoring Out a Common Factor
Factoring out a common factor is another way to rewrite an equation in Ax+By=C form. This method is useful when the equation has multiple terms with a common factor.
Consider the equation 2x + 6y = 12. To rewrite this equation in Ax+By=C form, we need to factor out a common factor of 2 from the x and y terms.
2(x + 3y) = 12
As you can see, the equation is now in Ax+By=C form, where A = 1, B = 3, and C = 6.

Method 5: Using Algebraic Manipulations
Finally, we can use algebraic manipulations such as combining like terms, canceling out terms, or using the distributive property to rewrite an equation in Ax+By=C form.
Consider the equation x + 2y + 3x = 7. To rewrite this equation in Ax+By=C form, we need to combine like terms and use the distributive property.
x + 3x + 2y = 7 4x + 2y = 7
As you can see, the equation is now in Ax+By=C form, where A = 4, B = 2, and C = 7.
Conclusion: Putting it all Together
Rewriting equations in Ax+By=C form is an essential skill in mathematics. By using the five methods outlined in this article, you can rewrite equations in this form with ease. Remember to rearrange terms, add or subtract the same value, multiply or divide by a constant, factor out a common factor, and use algebraic manipulations to rewrite equations in Ax+By=C form.
We hope this article has been informative and helpful in your mathematical journey. If you have any questions or comments, please feel free to share them below.
What is the Ax+By=C form of an equation?
+The Ax+By=C form of an equation is a linear equation where A, B, and C are constants, and x and y are variables.
Why is it important to rewrite equations in Ax+By=C form?
+Rewriting equations in Ax+By=C form makes it easier to solve them and visualize the relationship between the variables.
Can I use these methods to rewrite non-linear equations?
+No, these methods are specifically designed for rewriting linear equations in Ax+By=C form. Non-linear equations require different methods and techniques.