The importance of understanding numbers and their representations cannot be overstated. From finance to science, accurate calculations and representations are crucial for decision-making and problem-solving. One concept that is often overlooked, yet essential, is the representation of numbers in different forms. In this article, we will delve into the world of decimal forms, specifically exploring the concept of 60 in decimal form.
In everyday life, we often come across numbers that are represented in fractions or percentages. However, when dealing with complex calculations or measurements, it is essential to convert these numbers into decimal forms. Decimal forms provide a more precise and accurate way of representing numbers, which is vital in various fields such as mathematics, physics, and engineering.
So, what is 60 in decimal form? To answer this question, we need to understand the concept of decimal forms and how they work.
Understanding Decimal Forms
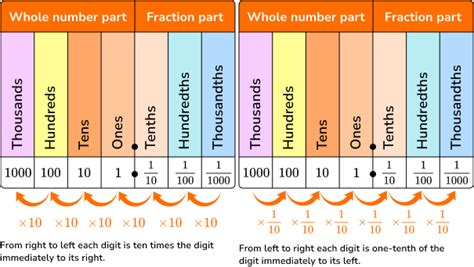
Decimal forms are a way of representing numbers using a point (.) to separate the whole part from the fractional part. This system allows us to express numbers with greater precision and accuracy. In decimal forms, each digit after the point represents a power of 10. For example, the number 0.5 can be read as "five-tenths" or "one-half."
Decimal forms are used extensively in mathematics, science, and finance to provide a more precise and accurate way of representing numbers. They are also used in everyday life, such as in measurements, conversions, and calculations.

Converting Fractions to Decimal Forms
To convert a fraction to a decimal form, we need to divide the numerator by the denominator. For example, to convert the fraction 1/2 to a decimal form, we divide 1 by 2, which gives us 0.5.
Similarly, to convert the number 60 to a decimal form, we need to divide 60 by 1, since 60 is a whole number. This gives us 60.0, which is the decimal form of 60.
However, in some cases, we may need to convert a fraction to a decimal form, where the numerator is greater than the denominator. In such cases, we can use a calculator or perform the division manually.
Benefits of Decimal Forms
Decimal forms have several benefits that make them an essential tool in various fields. Some of the benefits include:
- Precision and accuracy: Decimal forms provide a more precise and accurate way of representing numbers, which is vital in fields such as mathematics, physics, and engineering.
- Easy calculations: Decimal forms make calculations easier and faster, especially when dealing with complex numbers.
- Conversions: Decimal forms make conversions between different units easier, such as converting fractions to percentages.
- Comparisons: Decimal forms make comparisons between different numbers easier, especially when dealing with complex fractions.

Applications of Decimal Forms
Decimal forms have a wide range of applications in various fields, including:
- Mathematics: Decimal forms are used extensively in mathematics to provide a more precise and accurate way of representing numbers.
- Science: Decimal forms are used in science to measure and calculate complex phenomena, such as velocities, accelerations, and forces.
- Finance: Decimal forms are used in finance to calculate interest rates, investment returns, and currency conversions.
- Engineering: Decimal forms are used in engineering to design and calculate complex systems, such as bridges, buildings, and electronic circuits.
Common Decimal Forms
Some common decimal forms include:
- 0.5: One-half
- 0.25: One-quarter
- 0.1: One-tenth
- 0.01: One-hundredth
- 0.001: One-thousandth
These decimal forms are used extensively in everyday life, such as in measurements, conversions, and calculations.

Challenges and Limitations
While decimal forms provide a more precise and accurate way of representing numbers, they also have some challenges and limitations. Some of these include:
- Rounding errors: Decimal forms can be prone to rounding errors, especially when dealing with complex calculations.
- Conversion errors: Decimal forms can be prone to conversion errors, especially when converting between different units.
- Limited precision: Decimal forms have limited precision, especially when dealing with very large or very small numbers.
To overcome these challenges and limitations, it is essential to use calculators or software that can handle decimal forms accurately and precisely.
Conclusion
In conclusion, 60 in decimal form is 60.0. Decimal forms provide a more precise and accurate way of representing numbers, which is vital in various fields such as mathematics, physics, and engineering. They have several benefits, including precision and accuracy, easy calculations, conversions, and comparisons. Decimal forms have a wide range of applications in various fields, including mathematics, science, finance, and engineering.

We hope this article has provided you with a comprehensive understanding of decimal forms and their importance in various fields. If you have any questions or comments, please feel free to share them below.
What is the decimal form of 60?
+The decimal form of 60 is 60.0.
Why are decimal forms important?
+Decimal forms provide a more precise and accurate way of representing numbers, which is vital in various fields such as mathematics, physics, and engineering.
What are some common decimal forms?
+Some common decimal forms include 0.5, 0.25, 0.1, 0.01, and 0.001.