3 Sets Of Angles That Form A Triangle

Quick Links :

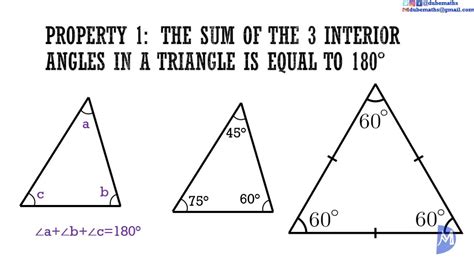
Triangles are a fundamental concept in geometry, and understanding the different types of angles that form a triangle is essential for various mathematical and real-world applications. In this article, we will delve into three sets of angles that form a triangle, exploring their characteristics, properties, and examples.

1. Acute, Right, and Obtuse Angles

The first set of angles that form a triangle consists of acute, right, and obtuse angles. These angles are classified based on their measure, which is the amount of rotation between the two sides of the angle.

• Acute Angle: An acute angle is an angle whose measure is less than 90 degrees. In a triangle, an acute angle is formed when two sides intersect, creating a sharp, pointed vertex.
• Right Angle: A right angle is an angle whose measure is exactly 90 degrees. In a triangle, a right angle is formed when two sides intersect, creating a perfect "L" shape.
• Obtuse Angle: An obtuse angle is an angle whose measure is greater than 90 degrees but less than 180 degrees. In a triangle, an obtuse angle is formed when two sides intersect, creating a wide, obtuse vertex.

These three types of angles can be combined to form different types of triangles. For example, a right triangle has one right angle and two acute angles, while an obtuse triangle has one obtuse angle and two acute angles.

Properties and Examples

• The sum of the measures of the angles in a triangle is always 180 degrees.
• In a right triangle, the Pythagorean theorem states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
• An obtuse triangle can be divided into two acute triangles by dropping a perpendicular from the obtuse vertex to the opposite side.

2. Interior and Exterior Angles

The second set of angles that form a triangle consists of interior and exterior angles. These angles are classified based on their position relative to the triangle.

• Interior Angle: An interior angle is an angle formed by two sides of a triangle. In other words, it is an angle that is "inside" the triangle.
• Exterior Angle: An exterior angle is an angle formed by one side of a triangle and an extension of an adjacent side. In other words, it is an angle that is "outside" the triangle.

These two types of angles are related by the exterior angle theorem, which states that the measure of an exterior angle is equal to the sum of the measures of the remote interior angles.

Properties and Examples

• The sum of the measures of the interior angles of a triangle is always 180 degrees.
• The sum of the measures of the exterior angles of a triangle is always 360 degrees.
• In a triangle, the exterior angle is equal to the sum of the remote interior angles.

3. Alternate Interior and Corresponding Angles

The third set of angles that form a triangle consists of alternate interior and corresponding angles. These angles are classified based on their position relative to a transversal line.

• Alternate Interior Angle: An alternate interior angle is an angle formed by a transversal line and a side of a triangle, such that the angle is on the opposite side of the transversal line from another angle.
• Corresponding Angle: A corresponding angle is an angle formed by a transversal line and a side of a triangle, such that the angle is on the same side of the transversal line as another angle.

These two types of angles are related by the alternate interior angle theorem, which states that alternate interior angles are equal, and the corresponding angle theorem, which states that corresponding angles are equal.

Properties and Examples

• In a triangle, alternate interior angles are equal.
• In a triangle, corresponding angles are equal.
• The alternate interior angle theorem and corresponding angle theorem can be used to solve problems involving angles in triangles.

In conclusion, these three sets of angles that form a triangle are essential concepts in geometry, and understanding their properties and relationships is crucial for solving various mathematical and real-world problems.

We hope this article has provided you with a deeper understanding of the different types of angles that form a triangle. Do you have any questions or comments about this topic? Share your thoughts with us in the comments section below!