5 Ways To Write A Hyperbola Equation In Standard Form

Quick Links :

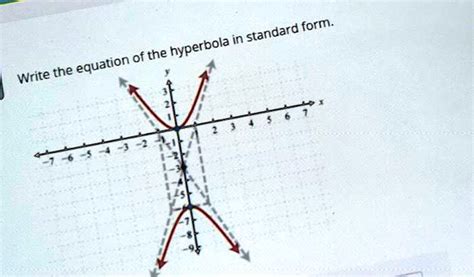
The hyperbola equation is a fundamental concept in mathematics, particularly in algebra and geometry. A hyperbola is a type of curve that has two separate parts, or branches, which are mirrored across a central line. Writing a hyperbola equation in standard form is crucial for understanding its properties and behavior.

Understanding the Hyperbola Equation

Before we dive into the ways to write a hyperbola equation in standard form, let's first understand the basic components of a hyperbola. A hyperbola has two axes: a transverse axis and a conjugate axis. The transverse axis is the longer axis, while the conjugate axis is the shorter axis. The center of the hyperbola is the point where the two axes intersect.

Standard Form of a Hyperbola Equation

The standard form of a hyperbola equation is:

(x^2/a^2) - (y^2/b^2) = 1

or

(y^2/a^2) - (x^2/b^2) = 1

where a and b are the lengths of the semi-transverse and semi-conjugate axes, respectively.

5 Ways to Write a Hyperbola Equation in Standard Form

Here are five ways to write a hyperbola equation in standard form:

1. Using the Distance Formula

One way to write a hyperbola equation in standard form is to use the distance formula. The distance formula is:

d = sqrt((x2 - x1)^2 + (y2 - y1)^2)

where d is the distance between two points (x1, y1) and (x2, y2).

To write a hyperbola equation using the distance formula, we need to find the distance between the center of the hyperbola and a point on the hyperbola.

2. Using the Slope-Intercept Form

Another way to write a hyperbola equation in standard form is to use the slope-intercept form. The slope-intercept form is:

y = mx + b

where m is the slope and b is the y-intercept.

To write a hyperbola equation using the slope-intercept form, we need to find the slope and y-intercept of the asymptotes of the hyperbola.

3. Using the Point-Slope Form

The point-slope form is another way to write a hyperbola equation in standard form. The point-slope form is:

y - y1 = m(x - x1)

where (x1, y1) is a point on the hyperbola and m is the slope.

To write a hyperbola equation using the point-slope form, we need to find a point on the hyperbola and the slope of the asymptotes.

4. Using the Parametric Equations

Parametric equations are another way to write a hyperbola equation in standard form. Parametric equations are:

x = a cosh(t) y = b sinh(t)

where a and b are the lengths of the semi-transverse and semi-conjugate axes, respectively, and t is a parameter.

To write a hyperbola equation using parametric equations, we need to find the values of a and b.

5. Using the Graphing Method

The graphing method is a visual way to write a hyperbola equation in standard form. To graph a hyperbola, we need to find the asymptotes and the vertices of the hyperbola.

To write a hyperbola equation using the graphing method, we need to find the equation of the asymptotes and the coordinates of the vertices.

Conclusion

Writing a hyperbola equation in standard form is a crucial step in understanding the properties and behavior of a hyperbola. There are five ways to write a hyperbola equation in standard form, each with its own advantages and disadvantages. By mastering these methods, you can become proficient in writing hyperbola equations and solving problems related to hyperbolas.

Final Thoughts

Writing a hyperbola equation in standard form is an essential skill in mathematics. By following these five methods, you can become proficient in writing hyperbola equations and solving problems related to hyperbolas. Remember to practice regularly and apply these methods to different types of hyperbolas.

Share Your Thoughts

We would love to hear your thoughts on writing hyperbola equations in standard form. Do you have any favorite methods or techniques? Share your experiences and tips in the comments section below.

FAQ Section