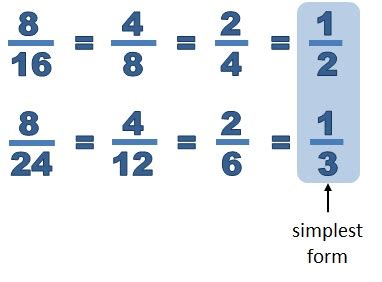35 As A Fraction In Simplest Form

Quick Links :

The concept of fractions is a fundamental aspect of mathematics, and simplifying fractions is an essential skill to master. In this article, we will delve into the world of fractions and explore how to express the number 35 as a fraction in its simplest form.

Understanding Fractions

A fraction is a way to represent a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, while the denominator tells us how many parts the whole is divided into. For example, the fraction 3/4 represents three equal parts out of a total of four parts.

Expressing 35 as a Fraction

To express 35 as a fraction, we need to find a denominator that divides 35 evenly. Since 35 is an integer, we can express it as a fraction with a denominator of 1, like this:

35/1

However, this is not a simplified fraction. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and denominator and divide both numbers by the GCD.

Simplifying the Fraction

The GCD of 35 and 1 is 1, which means that the fraction 35/1 is already in its simplest form. However, we can still express 35 as a fraction with a denominator greater than 1. For example:

35/1 = 35/5 = 7

In this example, we have divided both the numerator and denominator by 5, which is a common factor. This gives us the simplified fraction 7/1, which is equal to the original fraction 35/1.

Other Ways to Express 35 as a Fraction

There are other ways to express 35 as a fraction. For example:

35/1 = 70/2 = 105/3 = 140/4

In each of these examples, we have multiplied both the numerator and denominator by a different factor to create a new fraction that is equivalent to the original fraction.

Real-World Applications

Fractions are used in many real-world applications, such as cooking, finance, and science. For example, a recipe might call for 3/4 cup of flour, or a financial analyst might express a company's profit margin as a fraction. In science, fractions are used to express ratios and proportions, such as the ratio of a chemical compound's reactants to products.

Benefits of Simplifying Fractions

Simplifying fractions is an important skill to master, as it can help you to:

• Reduce errors in calculations
• Make calculations more efficient
• Improve your understanding of mathematical concepts
• Communicate mathematical ideas more effectively

Steps to Simplify a Fraction

To simplify a fraction, follow these steps:

1. Find the greatest common divisor (GCD) of the numerator and denominator.
2. Divide both the numerator and denominator by the GCD.
3. Repeat steps 1 and 2 until the fraction is in its simplest form.

Common Mistakes to Avoid

When simplifying fractions, there are several common mistakes to avoid:

• Dividing both the numerator and denominator by a factor that is not common to both numbers.
• Failing to check if the fraction is already in its simplest form.
• Not using the correct notation for fractions (e.g., using a slash instead of a division symbol).

Conclusion

In conclusion, expressing 35 as a fraction in its simplest form requires an understanding of fractions and the ability to simplify them. By following the steps outlined in this article, you can simplify fractions with confidence and accuracy. Remember to always check your work and avoid common mistakes to ensure that your fractions are in their simplest form.

Frequently Asked Questions