Simplify The Square Root Of 58 In 5 Easy Steps

Quick Links :

Simplifying square roots can be a bit tricky, but with the right approach, it can be done easily. In this article, we will explore the process of simplifying the square root of 58 in 5 easy steps. Whether you are a student, teacher, or simply someone who wants to improve their math skills, this article is for you.

The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16. However, not all numbers have a perfect square root, and that's where simplification comes in.

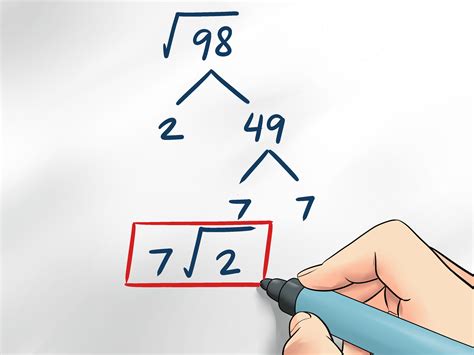
Step 1: Find the Prime Factorization of 58

To simplify the square root of 58, we need to start by finding its prime factorization. The prime factorization of a number is the expression of that number as the product of its prime factors. In this case, the prime factorization of 58 is:

58 = 2 x 29

What are Prime Factors?

Prime factors are prime numbers that, when multiplied together, give the original number. In this case, 2 and 29 are prime numbers, and when multiplied together, they give 58.

Step 2: Identify the Perfect Square Factors

Now that we have the prime factorization of 58, we need to identify the perfect square factors. A perfect square factor is a factor that is a perfect square. In this case, the only perfect square factor is 1.

Why are Perfect Square Factors Important?

Perfect square factors are important because they can be taken out of the square root, leaving a simpler expression. In this case, since 1 is a perfect square factor, we can take it out of the square root.

Step 3: Simplify the Square Root

Now that we have identified the perfect square factors, we can simplify the square root. Since 1 is a perfect square factor, we can take it out of the square root, leaving:

√58 = √(2 x 29) = √2 x √29 = √(2 x 29) = √(2)√(29)

How to Simplify Square Roots with Variables

Simplifying square roots with variables can be a bit more complicated, but the process is the same. We need to identify the perfect square factors and take them out of the square root.

Step 4: Combine the Terms

Now that we have simplified the square root, we can combine the terms. In this case, we have:

√58 = √(2 x 29) = √2 x √29

Since the square root of 2 and the square root of 29 are not perfect squares, we cannot simplify further.

Step 5: Write the Final Answer

And that's it! We have simplified the square root of 58 in 5 easy steps. The final answer is:

√58 = √(2 x 29) = √2 x √29

How to Use this Information in Real Life

Simplifying square roots is an important skill that can be used in real life. For example, if you are building a deck and need to calculate the length of a diagonal, you will need to simplify the square root of a number.

In conclusion, simplifying the square root of 58 is a straightforward process that requires identifying the perfect square factors and taking them out of the square root. By following these steps, you can simplify the square root of any number.

Do you have any questions about simplifying square roots? Share your thoughts in the comments below!