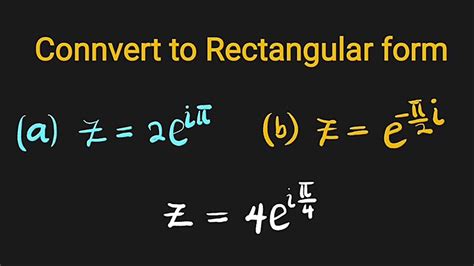Convert Rectangular To Exponential Form Easily

Quick Links :

Expressing complex numbers in different forms is essential in mathematics, engineering, and various fields. One such representation is the exponential form, which is a powerful tool for analyzing and working with complex numbers. In this article, we'll explore how to convert rectangular to exponential form easily, along with practical examples and a comprehensive guide.

Understanding Rectangular and Exponential Forms

Before diving into the conversion process, let's briefly review the rectangular and exponential forms of complex numbers.

• Rectangular form: A complex number in rectangular form is represented as z = a + bi, where 'a' is the real part and 'b' is the imaginary part.
• Exponential form: A complex number in exponential form is represented as z = re^(iθ), where 'r' is the magnitude (or length) and 'θ' is the angle (or argument).

Why Convert Rectangular to Exponential Form?

Converting complex numbers from rectangular to exponential form offers several advantages:

• Simplifies calculations: Exponential form makes it easier to perform operations like multiplication and division.
• Provides insight into complex number properties: Exponential form helps in understanding the magnitude and angle of complex numbers, which is crucial in various applications.
• Facilitates visual representation: Exponential form enables the representation of complex numbers on a polar coordinate system, making it easier to visualize and analyze.

Conversion Steps: Rectangular to Exponential Form

To convert a complex number from rectangular to exponential form, follow these steps:

1. Calculate the magnitude (r): The magnitude of a complex number is given by the formula: r = √(a^2 + b^2), where 'a' is the real part and 'b' is the imaginary part.
2. Calculate the angle (θ): The angle of a complex number can be calculated using the formula: θ = arctan(b/a), where 'a' is the real part and 'b' is the imaginary part.
3. Express the complex number in exponential form: Once you have the magnitude (r) and angle (θ), express the complex number in exponential form as z = re^(iθ).

Example 1: Convert 3 + 4i to Exponential Form

Let's convert the complex number 3 + 4i to exponential form:

1. Calculate the magnitude: r = √(3^2 + 4^2) = √(9 + 16) = √25 = 5
2. Calculate the angle: θ = arctan(4/3) = 53.13°
3. Express the complex number in exponential form: z = 5e^(i53.13°)

Example 2: Convert 2 - 5i to Exponential Form

Let's convert the complex number 2 - 5i to exponential form:

1. Calculate the magnitude: r = √(2^2 + (-5)^2) = √(4 + 25) = √29
2. Calculate the angle: θ = arctan(-5/2) = -68.2° (Note: The angle is negative because the imaginary part is negative)
3. Express the complex number in exponential form: z = √29e^(-i68.2°)

Common Applications of Exponential Form

Exponential form has numerous applications in various fields, including:

• Electrical engineering: Exponential form is used to analyze and design electrical circuits, particularly in the context of AC circuits.
• Signal processing: Exponential form is used to represent and manipulate signals in signal processing.
• Control systems: Exponential form is used to analyze and design control systems, particularly in the context of stability analysis.

Conclusion: Unlocking the Power of Exponential Form

In conclusion, converting complex numbers from rectangular to exponential form is a powerful technique that simplifies calculations, provides insight into complex number properties, and facilitates visual representation. By mastering this conversion, you'll unlock the full potential of exponential form and be better equipped to tackle complex problems in various fields.