5 Ways To Understand Radical Form Definition

Quick Links :

Understanding Radical Form Definition: Unlocking the Secrets of Algebra

Radical form definition is a fundamental concept in algebra that can be daunting for many students. However, with the right approach, it can be broken down into manageable parts, making it easier to understand and work with. In this article, we will explore five ways to understand radical form definition, providing you with a comprehensive guide to mastering this crucial concept.

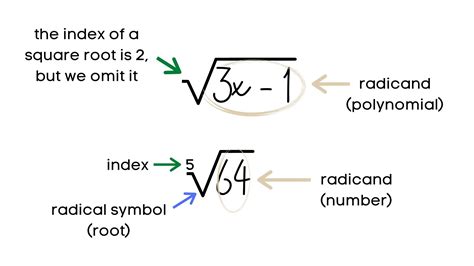
Radical form definition is a way of expressing a number or an algebraic expression using radicals, which are mathematical symbols used to represent roots or fractional exponents. Understanding radical form definition is essential for solving equations, simplifying expressions, and performing various mathematical operations.

The concept of radical form definition is often shrouded in mystery, leaving many students feeling frustrated and lost. However, by breaking it down into smaller, more manageable parts, you can develop a deeper understanding of this concept and become proficient in using it to solve a wide range of mathematical problems.

What is Radical Form Definition?

Radical form definition is a mathematical expression that uses radicals to represent a number or an algebraic expression. It is a way of writing a number or expression using a radical symbol, which is denoted by the symbol √. The radical symbol is used to represent the square root of a number or expression, but it can also be used to represent higher-order roots, such as cube roots or fourth roots.

Radical form definition is used to simplify complex expressions, solve equations, and perform various mathematical operations. It is a fundamental concept in algebra and is used extensively in mathematics, science, and engineering.

Types of Radicals

There are several types of radicals, each with its own unique properties and uses. The most common types of radicals include:

• Square roots: These are the most common type of radical and are denoted by the symbol √.
• Cube roots: These are used to represent the cube root of a number or expression and are denoted by the symbol ∛.
• Higher-order roots: These are used to represent higher-order roots, such as fourth roots or fifth roots, and are denoted by the symbol ⁴√ or ⁵√.

Method 1: Understanding Radical Form Definition through Visualization

One way to understand radical form definition is through visualization. By representing radicals graphically, you can develop a deeper understanding of how they work and how to manipulate them.

To visualize radicals, you can use a number line or a graph to represent the radical expression. This can help you to see how the radical expression behaves and how it relates to other mathematical concepts.

For example, you can use a number line to represent the square root of a number. By drawing a number line and marking the point corresponding to the square root, you can see how the square root behaves and how it relates to other numbers.

Method 2: Breaking Down Radical Form Definition into Simpler Parts

Another way to understand radical form definition is by breaking it down into simpler parts. By breaking down the radical expression into smaller, more manageable parts, you can develop a deeper understanding of how it works.

To break down radical form definition, you can start by identifying the radical symbol and the expression inside the radical. You can then simplify the expression inside the radical and rewrite it in a simpler form.

For example, you can break down the expression √(x^2 + 4) by simplifying the expression inside the radical. By factoring the expression x^2 + 4, you can rewrite it as (x + 2)(x - 2). You can then take the square root of the expression, resulting in √((x + 2)(x - 2)).

Simplifying Radical Expressions

Simplifying radical expressions is an essential part of understanding radical form definition. By simplifying the expression inside the radical, you can rewrite it in a simpler form and make it easier to work with.

To simplify radical expressions, you can use various techniques, such as factoring, canceling out common factors, and using the properties of radicals.

For example, you can simplify the expression √(x^2 + 4) by factoring the expression inside the radical. By factoring x^2 + 4, you can rewrite it as (x + 2)(x - 2). You can then take the square root of the expression, resulting in √((x + 2)(x - 2)).

Method 3: Using Real-World Examples to Illustrate Radical Form Definition

Using real-world examples is an effective way to illustrate radical form definition and make it more accessible. By using real-world examples, you can show how radical form definition is used in practical applications and how it can be used to solve real-world problems.

For example, you can use the concept of radical form definition to calculate the distance between two points on a map. By using the Pythagorean theorem and radical form definition, you can calculate the distance between the two points and represent it graphically.

Method 4: Practicing Radical Form Definition with Exercises and Quizzes

Practicing radical form definition with exercises and quizzes is an essential part of mastering this concept. By practicing with various types of problems and exercises, you can develop a deeper understanding of radical form definition and improve your skills.

To practice radical form definition, you can use online resources, such as math websites or apps, or work with a tutor or teacher. You can also use worksheets or practice tests to test your knowledge and identify areas where you need to improve.

Method 5: Learning from Online Resources and Video Tutorials

Learning from online resources and video tutorials is an effective way to learn about radical form definition. By watching video tutorials or online lessons, you can develop a deeper understanding of this concept and learn how to apply it in practical applications.

To learn from online resources, you can use websites, such as Khan Academy or Mathway, or watch video tutorials on YouTube or other video-sharing platforms. You can also use online textbooks or digital resources to learn more about radical form definition.

Conclusion

Understanding radical form definition is a fundamental concept in algebra that can be mastered with practice and patience. By using visualization, breaking down the expression into simpler parts, using real-world examples, practicing with exercises and quizzes, and learning from online resources and video tutorials, you can develop a deeper understanding of radical form definition and become proficient in using it to solve a wide range of mathematical problems.

Whether you are a student or a professional, mastering radical form definition can help you to improve your math skills and solve problems more efficiently. By following these five methods, you can unlock the secrets of radical form definition and become a master of algebra.