Angles are a fundamental concept in geometry, and understanding how they form and interact is crucial for various mathematical and real-world applications. One of the most important types of angles is the right angle, which measures exactly 90 degrees. In this article, we will explore five ways right angles form with perpendicular lines, along with their properties, examples, and practical applications.
What are Right Angles and Perpendicular Lines?

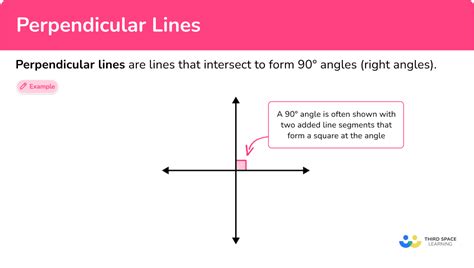
Right angles are angles that measure 90 degrees. They are formed when two lines intersect and create a sharp corner. Perpendicular lines, on the other hand, are lines that intersect at a right angle. In other words, when two lines are perpendicular, they form a right angle.
Properties of Right Angles and Perpendicular Lines
Right angles and perpendicular lines have several important properties:
- The sum of the angles in a triangle is always 180 degrees.
- When two lines are perpendicular, they form a right angle.
- Perpendicular lines have the same slope, but with opposite signs.
These properties are essential for understanding how right angles form with perpendicular lines.
1. Adjacent Angles

Adjacent angles are angles that share a common vertex and a common side. When two adjacent angles form a right angle, they are called adjacent right angles. This type of angle is formed when two perpendicular lines intersect.
Example: In a rectangle, the adjacent angles formed by the perpendicular sides are right angles.
2. Vertical Angles

Vertical angles are angles that are opposite each other when two lines intersect. When two perpendicular lines intersect, they form vertical angles that are right angles.
Example: In a diagram, when two perpendicular lines intersect, the vertical angles formed are right angles.
3. Alternate Interior Angles

Alternate interior angles are angles that are on opposite sides of a transversal line. When two perpendicular lines intersect, the alternate interior angles formed are right angles.
Example: In a diagram, when a transversal line intersects two perpendicular lines, the alternate interior angles formed are right angles.
4. Corresponding Angles

Corresponding angles are angles that are in the same relative position when two lines intersect. When two perpendicular lines intersect, the corresponding angles formed are right angles.
Example: In a diagram, when two perpendicular lines intersect, the corresponding angles formed are right angles.
5. Interior Angles of a Rectangle

A rectangle is a quadrilateral with four right angles. The interior angles of a rectangle are right angles, and they are formed by the perpendicular sides.
Example: In a rectangle, the interior angles are right angles, and they are formed by the perpendicular sides.
In conclusion, right angles and perpendicular lines are essential concepts in geometry, and they have various practical applications. By understanding how right angles form with perpendicular lines, we can solve various mathematical problems and real-world applications. We encourage you to practice and explore more about right angles and perpendicular lines.
What is a right angle?
+A right angle is an angle that measures exactly 90 degrees.
What are perpendicular lines?
+Perpendicular lines are lines that intersect at a right angle.
How do right angles form with perpendicular lines?
+Right angles form with perpendicular lines in five ways: adjacent angles, vertical angles, alternate interior angles, corresponding angles, and interior angles of a rectangle.