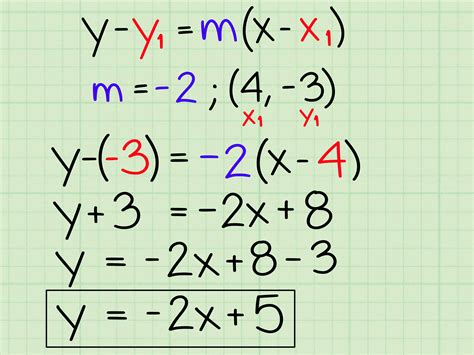Master Ixl Slope Intercept Form In 5 Easy Steps

Quick Links :

Mastering the slope-intercept form of a linear equation is a fundamental concept in mathematics, particularly in algebra and geometry. The slope-intercept form, denoted as y = mx + b, is a way of expressing a linear equation in terms of its slope (m) and y-intercept (b). In this article, we will guide you through 5 easy steps to master the slope-intercept form.

Understanding the Slope-Intercept Form

The slope-intercept form is a linear equation in the form of y = mx + b, where:

• m is the slope of the line, which represents the rate of change of the line
• b is the y-intercept, which is the point where the line intersects the y-axis
• x is the independent variable, which represents the input or the value on the x-axis
• y is the dependent variable, which represents the output or the value on the y-axis

Step 1: Identify the Slope (m)

To identify the slope (m) of a linear equation, you need to understand the concept of rise over run. The slope (m) is calculated as the ratio of the vertical change (rise) to the horizontal change (run). In other words, it measures how steep the line is.

For example, if you have two points on a line, (x1, y1) and (x2, y2), you can calculate the slope (m) using the formula:

m = (y2 - y1) / (x2 - x1)

Example:

Find the slope (m) of the line that passes through the points (2, 3) and (4, 5).

m = (5 - 3) / (4 - 2) = 2 / 2 = 1

Therefore, the slope (m) of the line is 1.

Step 2: Identify the Y-Intercept (b)

To identify the y-intercept (b) of a linear equation, you need to find the point where the line intersects the y-axis. The y-intercept (b) is the value of y when x is equal to 0.

For example, if you have a linear equation in the form of y = mx + b, you can find the y-intercept (b) by substituting x = 0 into the equation.

Example:

Find the y-intercept (b) of the line y = 2x + 3.

To find the y-intercept (b), substitute x = 0 into the equation:

y = 2(0) + 3 = 3

Therefore, the y-intercept (b) of the line is 3.

Step 3: Write the Equation in Slope-Intercept Form

Now that you have identified the slope (m) and y-intercept (b), you can write the equation in slope-intercept form.

For example, if you have a linear equation with a slope (m) of 2 and a y-intercept (b) of 3, you can write the equation as:

y = 2x + 3

Step 4: Graph the Line

To graph the line, you can use the slope-intercept form of the equation. First, plot the y-intercept (b) on the y-axis. Then, use the slope (m) to find another point on the line.

For example, if you have a linear equation y = 2x + 3, you can plot the y-intercept (b) of 3 on the y-axis. Then, use the slope (m) of 2 to find another point on the line.

Example:

Graph the line y = 2x + 3.

Plot the y-intercept (b) of 3 on the y-axis. Then, use the slope (m) of 2 to find another point on the line. For example, if x = 1, y = 2(1) + 3 = 5. Therefore, the point (1, 5) is on the line.

Step 5: Check Your Work

Finally, check your work by plugging in values for x and y to ensure that the equation is true.

For example, if you have a linear equation y = 2x + 3, you can plug in values for x and y to check your work.

Example:

Check the equation y = 2x + 3 by plugging in x = 2 and y = 7.

2x + 3 = 7 2(2) + 3 = 7 4 + 3 = 7 7 = 7

Therefore, the equation is true.

By following these 5 easy steps, you can master the slope-intercept form of a linear equation. Remember to identify the slope (m) and y-intercept (b), write the equation in slope-intercept form, graph the line, and check your work.

We hope this article has helped you master the slope-intercept form of a linear equation. Remember to practice, practice, practice to become proficient in using this concept. If you have any questions or need further clarification, please don't hesitate to ask.