5 Ways To Convert Quadratic Equations To Standard Form

Quick Links :

Converting quadratic equations to standard form is an essential skill in algebra, as it allows us to easily identify the key features of a quadratic function, such as the vertex, axis of symmetry, and x-intercepts. In this article, we will explore five ways to convert quadratic equations to standard form, providing you with a comprehensive understanding of the topic.

Understanding Standard Form

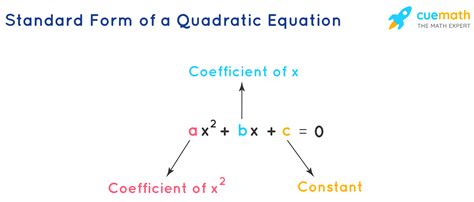
Before we dive into the methods, let's quickly review what standard form is. A quadratic equation in standard form is written in the form ax^2 + bx + c = 0, where a, b, and c are constants, and a ≠ 0. This form makes it easy to identify the key features of the quadratic function.

Method 1: Factoring

Factoring is a popular method for converting quadratic equations to standard form. To factor a quadratic equation, we need to find two binomials whose product equals the original equation. For example, let's say we have the equation x^2 + 5x + 6 = 0. We can factor this equation as (x + 3)(x + 2) = 0.

How to Factor a Quadratic Equation

To factor a quadratic equation, follow these steps:

1. Look for two numbers whose product equals the constant term (c) and whose sum equals the coefficient of the x term (b).
2. Write the factored form of the equation as the product of two binomials.
3. Check your work by multiplying the binomials to ensure they equal the original equation.

For example, let's say we have the equation x^2 + 7x + 12 = 0. We can factor this equation as (x + 3)(x + 4) = 0.

Method 2: Completing the Square

Completing the square is another method for converting quadratic equations to standard form. This method involves adding and subtracting a constant term to create a perfect square trinomial. For example, let's say we have the equation x^2 + 6x + 8 = 0. We can complete the square by adding and subtracting 9 to get (x^2 + 6x + 9) - 1 = 0.

How to Complete the Square

To complete the square, follow these steps:

1. Move the constant term to the right side of the equation.
2. Add and subtract (b/2)^2 to the left side of the equation.
3. Factor the perfect square trinomial.
4. Simplify the equation.

For example, let's say we have the equation x^2 + 4x + 5 = 0. We can complete the square by adding and subtracting 4 to get (x^2 + 4x + 4) + 1 = 0.

Method 3: Using the Quadratic Formula

The quadratic formula is a powerful tool for converting quadratic equations to standard form. The quadratic formula is x = (-b ± √(b^2 - 4ac)) / 2a. For example, let's say we have the equation x^2 + 3x + 2 = 0. We can use the quadratic formula to find the roots of the equation.

How to Use the Quadratic Formula

To use the quadratic formula, follow these steps:

1. Identify the values of a, b, and c in the equation.
2. Plug these values into the quadratic formula.
3. Simplify the expression to find the roots of the equation.

For example, let's say we have the equation x^2 + 2x + 1 = 0. We can use the quadratic formula to find the roots of the equation.

Method 4: Graphing

Graphing is a visual method for converting quadratic equations to standard form. By graphing the equation, we can identify the vertex, axis of symmetry, and x-intercepts. For example, let's say we have the equation x^2 + 4x + 4 = 0. We can graph this equation to find the vertex and x-intercepts.

How to Graph a Quadratic Equation

To graph a quadratic equation, follow these steps:

1. Identify the vertex of the parabola.
2. Identify the axis of symmetry.
3. Identify the x-intercepts.
4. Plot the points on a coordinate plane.

For example, let's say we have the equation x^2 + 2x + 1 = 0. We can graph this equation to find the vertex and x-intercepts.

Method 5: Using Algebraic Manipulation

Algebraic manipulation is a method for converting quadratic equations to standard form by using algebraic properties. For example, let's say we have the equation x^2 + 3x + 2 = 0. We can use algebraic manipulation to rewrite the equation in standard form.

How to Use Algebraic Manipulation

To use algebraic manipulation, follow these steps:

1. Identify the equation and the desired form.
2. Use algebraic properties to rewrite the equation.
3. Simplify the expression to get the standard form.

For example, let's say we have the equation x^2 + 2x + 1 = 0. We can use algebraic manipulation to rewrite the equation in standard form.

In conclusion, converting quadratic equations to standard form is an essential skill in algebra. By using factoring, completing the square, the quadratic formula, graphing, or algebraic manipulation, we can easily identify the key features of a quadratic function. Remember to practice each method to become proficient in converting quadratic equations to standard form.

Take Action

• Practice converting quadratic equations to standard form using each of the five methods.
• Use online resources or worksheets to practice converting quadratic equations.
• Share this article with a friend or classmate who is struggling with converting quadratic equations.