Unlocking the Power of Exponential and Logarithmic Functions

Exponential and logarithmic functions are fundamental concepts in mathematics, and understanding their relationship is crucial for solving various problems in algebra, calculus, and other fields. One of the essential skills in working with these functions is converting between exponential and logarithmic forms. In this article, we will explore the process of converting exponential forms to logarithmic forms and provide you with practical examples and tips to make this process easier.
The exponential form and logarithmic form are two different ways of expressing the same mathematical relationship. The exponential form represents a relationship between a base and an exponent, while the logarithmic form represents the inverse relationship between a base and its logarithm. Understanding the connection between these two forms is essential for solving problems in various mathematical and scientific contexts.
Why is Converting Exponential Forms to Logarithmic Forms Important?
Converting exponential forms to logarithmic forms is crucial in many mathematical and scientific applications. Logarithmic functions are often used to model real-world phenomena, such as population growth, chemical reactions, and electrical circuits. By converting exponential forms to logarithmic forms, you can simplify complex equations, solve problems more efficiently, and gain a deeper understanding of the underlying mathematical relationships.
Understanding the Basics of Exponential and Logarithmic Functions

Before we dive into the conversion process, let's review the basics of exponential and logarithmic functions.
An exponential function is a mathematical function of the form:
f(x) = ab^x
where a is a constant, b is the base, and x is the exponent.
A logarithmic function, on the other hand, is the inverse of an exponential function and is defined as:
f(x) = log_b(x)
where b is the base and x is the argument.
The key property of logarithmic functions is that they satisfy the following equation:
b^log_b(x) = x
This property allows us to convert exponential forms to logarithmic forms and vice versa.
Converting Exponential Forms to Logarithmic Forms
Now that we have reviewed the basics of exponential and logarithmic functions, let's explore the process of converting exponential forms to logarithmic forms.
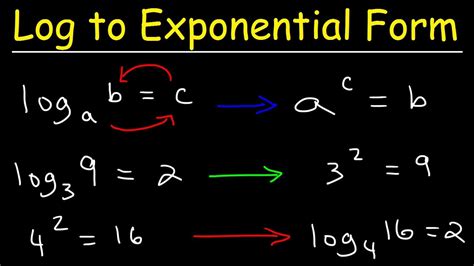
The general formula for converting an exponential form to a logarithmic form is:
b^x = y --> log_b(y) = x
where b is the base, x is the exponent, and y is the result.
Here are some examples to illustrate this process:
Example 1: 2^3 = 8 --> log_2(8) = 3
Example 2: 10^2 = 100 --> log_10(100) = 2
Example 3: e^4 = 54.598 --> log_e(54.598) = 4
As you can see, the process of converting exponential forms to logarithmic forms involves using the logarithmic function to "undo" the exponential function.
Practical Applications of Exponential and Logarithmic Functions

Exponential and logarithmic functions have numerous practical applications in various fields, including:
- Population growth and demographics
- Chemical reactions and kinetics
- Electrical circuits and electronics
- Finance and economics
- Computer science and programming
Understanding the relationship between exponential and logarithmic functions is essential for solving problems in these fields.
Tips and Tricks for Converting Exponential Forms to Logarithmic Forms
Here are some tips and tricks to help you master the process of converting exponential forms to logarithmic forms:
- Use the general formula: b^x = y --> log_b(y) = x
- Practice, practice, practice: The more you practice converting exponential forms to logarithmic forms, the more comfortable you will become with the process.
- Use logarithmic properties: Logarithmic properties, such as the product rule and the quotient rule, can help you simplify complex logarithmic expressions.
- Use online resources: There are many online resources, such as calculators and conversion tools, that can help you convert exponential forms to logarithmic forms.
By following these tips and tricks, you can become proficient in converting exponential forms to logarithmic forms and improve your problem-solving skills in mathematics and science.
Conclusion: Mastering the Art of Converting Exponential Forms to Logarithmic Forms

Converting exponential forms to logarithmic forms is a fundamental skill in mathematics and science. By understanding the relationship between exponential and logarithmic functions, you can simplify complex equations, solve problems more efficiently, and gain a deeper understanding of the underlying mathematical relationships.
We hope that this article has provided you with a comprehensive guide to converting exponential forms to logarithmic forms. With practice and persistence, you can master this skill and improve your problem-solving abilities in mathematics and science.
We encourage you to share your thoughts and experiences with converting exponential forms to logarithmic forms in the comments section below.
FAQ Section:
What is the general formula for converting exponential forms to logarithmic forms?
+The general formula for converting exponential forms to logarithmic forms is: b^x = y --> log_b(y) = x
Why is converting exponential forms to logarithmic forms important?
+Converting exponential forms to logarithmic forms is crucial in many mathematical and scientific applications, such as population growth, chemical reactions, and electrical circuits.
What are some tips and tricks for converting exponential forms to logarithmic forms?
+Some tips and tricks for converting exponential forms to logarithmic forms include using the general formula, practicing regularly, using logarithmic properties, and using online resources.