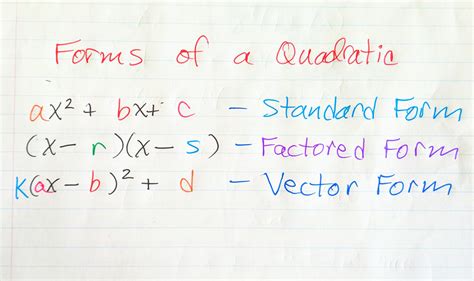Write Quadratic Functions In Standard Form Easily

Quick Links :

Quadratic functions are a fundamental concept in algebra and mathematics, and expressing them in standard form is a crucial skill for any student or professional. In this article, we will delve into the world of quadratic functions, explore their importance, and provide a step-by-step guide on how to write them in standard form with ease.

Quadratic functions are polynomial functions of degree two, which means the highest power of the variable is two. They are commonly expressed in the form of f(x) = ax^2 + bx + c, where a, b, and c are constants, and x is the variable. Quadratic functions have numerous applications in various fields, including physics, engineering, economics, and computer science.

The importance of quadratic functions lies in their ability to model real-world phenomena, such as the trajectory of a projectile, the shape of a mirror, or the behavior of a population. Quadratic functions can also be used to solve problems involving optimization, where the goal is to find the maximum or minimum value of a function.

Writing Quadratic Functions in Standard Form

The standard form of a quadratic function is f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola. This form is particularly useful for graphing and analyzing quadratic functions.

Here are the steps to write a quadratic function in standard form:

Step 1: Identify the Vertex

The vertex of a quadratic function is the point where the parabola changes direction. To identify the vertex, we need to find the values of h and k. The value of h is the x-coordinate of the vertex, while the value of k is the y-coordinate.

Method 1: Using the Vertex Formula

The vertex formula is given by:

h = -b / 2a k = f(h)

where a, b, and c are the coefficients of the quadratic function.

Method 2: Completing the Square

Completing the square is a technique used to rewrite a quadratic expression in the form of a perfect square trinomial.

For example, consider the quadratic function f(x) = x^2 + 6x + 8. To complete the square, we need to add and subtract a constant term:

f(x) = x^2 + 6x + 8 = x^2 + 6x + 9 - 1 = (x + 3)^2 - 1

Comparing this with the standard form, we can see that the vertex is (-3, -1).

Step 2: Write the Quadratic Function in Standard Form

Once we have identified the vertex, we can write the quadratic function in standard form. The general form of a quadratic function in standard form is:

f(x) = a(x - h)^2 + k

For example, consider the quadratic function f(x) = x^2 + 6x + 8. We have already found the vertex to be (-3, -1). Therefore, we can write the quadratic function in standard form as:

f(x) = (x + 3)^2 - 1

Step 3: Verify the Quadratic Function

To verify the quadratic function, we can substitute the values of x into the equation and check if the resulting values match the original function.

For example, consider the quadratic function f(x) = (x + 3)^2 - 1. We can substitute x = 0 into the equation and check if the resulting value matches the original function:

f(0) = (0 + 3)^2 - 1 = 9 - 1 = 8

Comparing this with the original function, we can see that the values match.

Tips and Tricks

• Always identify the vertex before writing the quadratic function in standard form.
• Use the vertex formula or complete the square to find the vertex.
• Verify the quadratic function by substituting values of x into the equation.
• Use the standard form to graph and analyze quadratic functions.

Conclusion Writing quadratic functions in standard form is a crucial skill in algebra and mathematics. By following the steps outlined in this article, you can easily write quadratic functions in standard form and analyze their behavior. Remember to identify the vertex, complete the square, and verify the quadratic function to ensure accuracy.

We hope this article has helped you understand the concept of quadratic functions in standard form. If you have any questions or need further clarification, please don't hesitate to comment below.