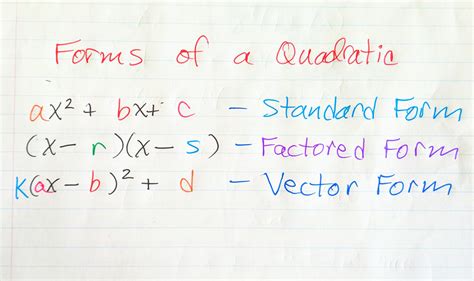Write Quadratic Functions In Standard Form Easily

Quick Links :

Quadratic functions are a crucial part of algebra and are used to model a wide range of real-world phenomena, from the trajectory of a thrown ball to the growth of a population. In this article, we'll explore how to write quadratic functions in standard form, a fundamental concept in mathematics that can seem daunting at first, but is actually quite straightforward.

The importance of quadratic functions cannot be overstated. They are used to describe phenomena that involve a squared variable, such as the area of a rectangle, the volume of a cylinder, or the motion of an object under the influence of gravity. By mastering quadratic functions, students can gain a deeper understanding of the world around them and develop problem-solving skills that can be applied in a variety of contexts.

But, what exactly is a quadratic function in standard form? Simply put, it is a polynomial function of degree two, which means the highest power of the variable (usually x) is two. In standard form, a quadratic function is written as ax^2 + bx + c, where a, b, and c are constants, and x is the variable.

Understanding the Components of a Quadratic Function

To write a quadratic function in standard form, it's essential to understand the components that make up the function. Let's break down the standard form of a quadratic function:

• ax^2: This is the quadratic term, where a is the coefficient and x^2 is the variable raised to the power of two. The coefficient a determines the direction and width of the parabola.
• bx: This is the linear term, where b is the coefficient and x is the variable. The coefficient b determines the position of the parabola on the x-axis.
• c: This is the constant term, which determines the position of the parabola on the y-axis.

The Role of Coefficients in Quadratic Functions

The coefficients a, b, and c play a crucial role in determining the shape and position of the parabola. Let's explore the role of each coefficient in more detail:

• a: The coefficient a determines the direction and width of the parabola. If a is positive, the parabola opens upwards, and if a is negative, it opens downwards. The greater the absolute value of a, the narrower the parabola.
• b: The coefficient b determines the position of the parabola on the x-axis. If b is positive, the parabola is shifted to the right, and if b is negative, it is shifted to the left.
• c: The constant term c determines the position of the parabola on the y-axis. If c is positive, the parabola is shifted upwards, and if c is negative, it is shifted downwards.

Steps to Write Quadratic Functions in Standard Form

Now that we've explored the components of a quadratic function, let's walk through the steps to write quadratic functions in standard form:

1. Identify the coefficients a, b, and c.
2. Write the quadratic term ax^2.
3. Write the linear term bx.
4. Write the constant term c.
5. Combine the terms to form the quadratic function in standard form.

For example, suppose we want to write the quadratic function that represents the area of a rectangle with a length of x + 2 and a width of x - 3. The area of the rectangle is given by the product of the length and width:

Area = (x + 2)(x - 3)

To write this function in standard form, we need to multiply the terms:

Area = x^2 - 3x + 2x - 6

Combine like terms:

Area = x^2 - x - 6

Now we have the quadratic function in standard form: x^2 - x - 6.

Real-World Applications of Quadratic Functions

Quadratic functions have numerous real-world applications in fields such as physics, engineering, economics, and computer science. Here are a few examples:

• Projectile motion: Quadratic functions are used to model the trajectory of projectiles, such as the path of a thrown ball or the trajectory of a missile.
• Electrical circuits: Quadratic functions are used to model the behavior of electrical circuits, including the voltage and current in a circuit.
• Population growth: Quadratic functions are used to model the growth of populations, including the growth of bacteria and the spread of diseases.

Common Challenges When Writing Quadratic Functions

When writing quadratic functions in standard form, students often encounter several common challenges. Here are a few:

• Forgetting to combine like terms: When multiplying out the terms, it's essential to combine like terms to simplify the expression.
• Incorrectly ordering the terms: The terms in a quadratic function should be ordered from highest to lowest power.
• Forgetting the constant term: The constant term c is essential to the quadratic function, so make sure to include it.

Tips and Strategies for Writing Quadratic Functions

Here are a few tips and strategies to help you write quadratic functions in standard form:

• Use a consistent method: Develop a consistent method for writing quadratic functions, such as using a template or following a set of steps.
• Check your work: Always check your work by plugging in values for x to ensure the function is correct.
• Practice, practice, practice: The more you practice writing quadratic functions, the more comfortable you'll become with the process.

Conclusion

Writing quadratic functions in standard form is a fundamental concept in mathematics that can seem daunting at first, but is actually quite straightforward. By understanding the components of a quadratic function, following the steps to write the function, and practicing regularly, you'll become proficient in no time. Remember to check your work, use a consistent method, and practice regularly to become a pro at writing quadratic functions.