2 Key Ways To Write Linear Equations

Quick Links :

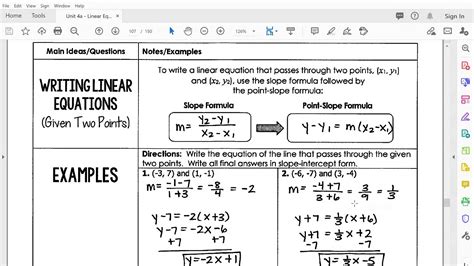
Linear equations are a fundamental concept in mathematics, and being able to write them is an essential skill for students and professionals alike. A linear equation is a mathematical statement that describes a relationship between two variables, typically represented as x and y. In this article, we will explore two key ways to write linear equations, providing you with a comprehensive understanding of this crucial math concept.

What are Linear Equations?

Linear equations are mathematical statements that describe a relationship between two variables, usually x and y. They are called "linear" because the graph of the equation is a straight line. Linear equations can be written in various forms, but they are often represented in the slope-intercept form, y = mx + b, where m is the slope of the line and b is the y-intercept.

Method 1: Writing Linear Equations in Slope-Intercept Form

The slope-intercept form of a linear equation is y = mx + b, where m is the slope of the line and b is the y-intercept. To write a linear equation in slope-intercept form, you need to know the slope and the y-intercept of the line.

• The slope (m) represents the rate of change of the line. It tells you how steep the line is.
• The y-intercept (b) is the point where the line crosses the y-axis.

For example, let's say you want to write a linear equation with a slope of 2 and a y-intercept of 3. The equation would be y = 2x + 3.

Example 1: Writing a Linear Equation in Slope-Intercept Form

Write a linear equation with a slope of 4 and a y-intercept of -2.

Solution: y = 4x - 2

Example 2: Writing a Linear Equation in Slope-Intercept Form

Write a linear equation with a slope of -3 and a y-intercept of 5.

Solution: y = -3x + 5

Method 2: Writing Linear Equations in Standard Form

The standard form of a linear equation is Ax + By = C, where A, B, and C are constants. To write a linear equation in standard form, you need to know the coefficients of x and y and the constant term.

• The coefficients of x and y (A and B) represent the rates of change of the line in the x and y directions.
• The constant term (C) is the value of the equation when x and y are both zero.

For example, let's say you want to write a linear equation with a coefficient of 2 for x, a coefficient of 3 for y, and a constant term of -4. The equation would be 2x + 3y = -4.

Example 1: Writing a Linear Equation in Standard Form

Write a linear equation with a coefficient of 4 for x, a coefficient of -2 for y, and a constant term of 6.

Solution: 4x - 2y = 6

Example 2: Writing a Linear Equation in Standard Form

Write a linear equation with a coefficient of -3 for x, a coefficient of 5 for y, and a constant term of -8.

Solution: -3x + 5y = -8

Key Differences Between Slope-Intercept Form and Standard Form

While both slope-intercept form and standard form can be used to write linear equations, there are key differences between the two.

• Slope-intercept form is often easier to use when you know the slope and y-intercept of the line.
• Standard form is often easier to use when you know the coefficients of x and y and the constant term.
• Slope-intercept form is more useful for graphing linear equations, as it provides the slope and y-intercept directly.
• Standard form is more useful for solving systems of linear equations, as it provides the coefficients of x and y and the constant term.

Conclusion

Writing linear equations is an essential skill in mathematics, and there are two key ways to do it: slope-intercept form and standard form. By understanding the differences between these two forms, you can choose the best approach for your specific needs. Whether you're working with slope-intercept form or standard form, the key is to understand the relationships between the variables and the constants.

We hope this article has provided you with a comprehensive understanding of linear equations and how to write them in two key forms. If you have any questions or comments, please don't hesitate to reach out. Share this article with your friends and colleagues, and let's keep the conversation going!