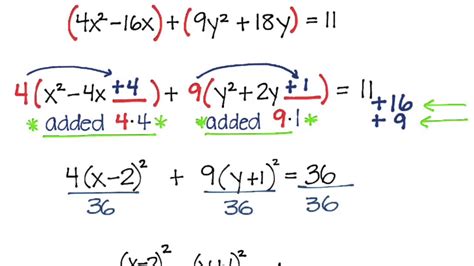The standard form of an ellipse is a fundamental concept in mathematics, particularly in geometry and algebra. It provides a clear and concise way to express the properties of an ellipse. However, converting a general equation to standard ellipse form can be a daunting task for many students and professionals alike. In this article, we will explore the steps and techniques to easily convert a general equation to standard ellipse form.
Understanding the Standard Ellipse Form

The standard form of an ellipse is given by:
(x - h)^2 / a^2 + (y - k)^2 / b^2 = 1
where (h, k) is the center of the ellipse, and a and b are the lengths of the semi-major and semi-minor axes, respectively. This form provides a clear and concise way to express the properties of an ellipse.
Importance of Converting to Standard Ellipse Form
Converting a general equation to standard ellipse form is essential in various mathematical and real-world applications. Some of the key benefits include:
- Easy identification of the center, vertices, and axes of the ellipse
- Simplified calculations for perimeter, area, and other properties
- Facilitated transformations and manipulations of the ellipse
- Enhanced visualization and graphing of the ellipse
Steps to Convert a General Equation to Standard Ellipse Form

To convert a general equation to standard ellipse form, follow these steps:
- Rearrange the equation: Rearrange the equation to isolate the terms involving x and y on one side of the equation.
- Complete the square: Complete the square for both x and y terms by adding and subtracting the appropriate constants.
- Factor the equation: Factor the equation to express it in the standard form.
Example 1: Converting a Simple Ellipse Equation
Consider the equation:
x^2 + 4y^2 = 16
To convert this equation to standard ellipse form, follow the steps:
- Rearrange the equation:
x^2 + 4y^2 - 16 = 0
- Complete the square:
(x^2 - 4) + 4(y^2 - 4) = 0
- Factor the equation:
(x - 2)^2 / 4 + (y - 0)^2 / 4 = 1
The resulting equation is in the standard ellipse form.
Common Challenges and Solutions

Some common challenges when converting a general equation to standard ellipse form include:
- Incorrect completion of squares: Make sure to add and subtract the correct constants when completing the square.
- Incorrect factoring: Double-check the factoring of the equation to ensure it is correct.
Example 2: Converting a More Complex Ellipse Equation
Consider the equation:
x^2 + 2y^2 - 4x + 6y = 10
To convert this equation to standard ellipse form, follow the steps:
- Rearrange the equation:
x^2 - 4x + 2y^2 + 6y - 10 = 0
- Complete the square:
(x^2 - 4x + 4) + 2(y^2 + 3y + 9/4) - 10 - 4 - 9/2 = 0
- Factor the equation:
(x - 2)^2 / 4 + (y + 3/2)^2 / 2 = 1
The resulting equation is in the standard ellipse form.
Conclusion: Mastering the Art of Conversion
Converting a general equation to standard ellipse form is a valuable skill in mathematics and real-world applications. By following the steps and techniques outlined in this article, you can easily convert any general equation to standard ellipse form. Remember to pay attention to common challenges and solutions, and practice regularly to master the art of conversion.
We hope this article has been informative and helpful. If you have any questions or comments, please feel free to share them below.
What is the standard form of an ellipse?
+The standard form of an ellipse is (x - h)^2 / a^2 + (y - k)^2 / b^2 = 1, where (h, k) is the center of the ellipse, and a and b are the lengths of the semi-major and semi-minor axes, respectively.
Why is it important to convert a general equation to standard ellipse form?
+Converting a general equation to standard ellipse form provides a clear and concise way to express the properties of an ellipse, making it easier to identify the center, vertices, and axes, and facilitating calculations and transformations.
What are some common challenges when converting a general equation to standard ellipse form?
+Common challenges include incorrect completion of squares and incorrect factoring. It is essential to double-check the calculations and factoring to ensure the correct conversion.