Distance Between Two Points In Simplest Radical Form

Quick Links :

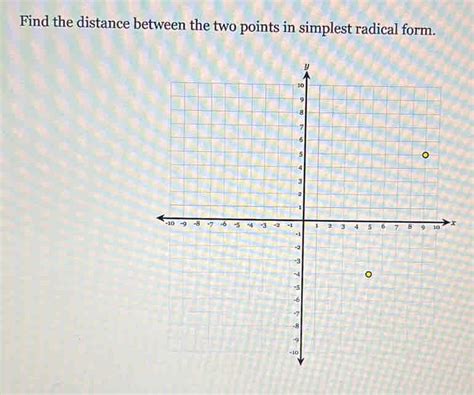
The distance between two points is a fundamental concept in mathematics, particularly in geometry and trigonometry. It is used to calculate the length of the line segment connecting two points in a coordinate plane. In this article, we will explore the concept of distance between two points, its importance, and how to calculate it in simplest radical form.

Understanding the Concept of Distance Between Two Points

The distance between two points is defined as the length of the line segment connecting them. It is a measure of how far apart two points are in a coordinate plane. The concept of distance is crucial in various fields, such as physics, engineering, and computer science, where it is used to calculate distances between objects, velocities, and trajectories.

Importance of Distance Between Two Points

The distance between two points has numerous applications in real-life scenarios. For instance, in physics, it is used to calculate the distance between two objects, which is essential in determining their relative motion and velocity. In engineering, it is used to calculate the distance between two points on a map or a blueprint, which is crucial in designing and building structures.

Calculating Distance Between Two Points

The distance between two points can be calculated using the distance formula, which is derived from the Pythagorean theorem. The distance formula is:

d = √((x2 - x1)^2 + (y2 - y1)^2)

where d is the distance between the two points, (x1, y1) and (x2, y2) are the coordinates of the two points.

Steps to Calculate Distance Between Two Points

To calculate the distance between two points, follow these steps:

1. Identify the coordinates of the two points.
2. Plug the coordinates into the distance formula.
3. Simplify the equation by squaring the differences between the x-coordinates and the y-coordinates.
4. Add the squared differences together.
5. Take the square root of the sum.

Calculating Distance in Simplest Radical Form

To calculate the distance in simplest radical form, follow these steps:

1. Calculate the distance using the distance formula.
2. Simplify the equation by factoring out any perfect squares.
3. Take the square root of the simplified equation.

Example of Calculating Distance in Simplest Radical Form

Suppose we want to calculate the distance between the points (3, 4) and (6, 8). Using the distance formula, we get:

d = √((6 - 3)^2 + (8 - 4)^2) = √(3^2 + 4^2) = √(9 + 16) = √25 = 5

Therefore, the distance between the points (3, 4) and (6, 8) is 5 units.

Practical Applications of Distance Between Two Points

The distance between two points has numerous practical applications in various fields. For instance:

• In physics, it is used to calculate the distance between two objects, which is essential in determining their relative motion and velocity.
• In engineering, it is used to calculate the distance between two points on a map or a blueprint, which is crucial in designing and building structures.
• In computer science, it is used to calculate the distance between two points in a graphical user interface, which is essential in designing and building graphical applications.

Real-Life Scenarios of Distance Between Two Points

The distance between two points has numerous real-life scenarios, such as:

• Calculating the distance between two cities on a map.
• Determining the distance between two objects in a room.
• Calculating the distance between two points on a blueprint.

In conclusion, the distance between two points is a fundamental concept in mathematics, particularly in geometry and trigonometry. It is used to calculate the length of the line segment connecting two points in a coordinate plane. By following the steps outlined in this article, you can calculate the distance between two points in simplest radical form. Whether you are a student, a teacher, or a professional, understanding the concept of distance between two points is essential in various fields and real-life scenarios.