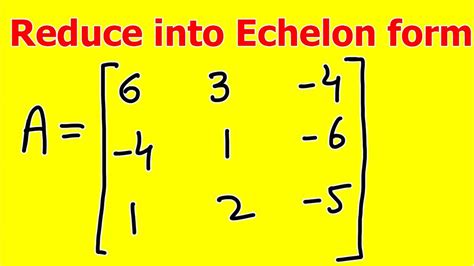
Echelon form calculators have revolutionized the way we approach matrix operations, making it easier than ever to perform complex calculations with ease. In this article, we will delve into the world of echelon form calculators, exploring their benefits, working mechanisms, and steps involved in using them.
What is Echelon Form?

Echelon form, also known as row echelon form, is a simplified form of a matrix where all the elements below the leading entry (also known as the pivot) are zeros. This form is particularly useful for solving systems of linear equations, as it allows for easy identification of the solution.
Benefits of Echelon Form Calculators
Echelon form calculators offer a range of benefits, including:
- Easy matrix reduction: Echelon form calculators simplify the process of reducing a matrix to its row echelon form, making it easier to solve systems of linear equations.
- Time-saving: By automating the process of matrix reduction, echelon form calculators save time and effort, allowing users to focus on other tasks.
- Accuracy: Echelon form calculators eliminate the risk of human error, ensuring accurate results every time.
- Convenience: Online echelon form calculators can be accessed from anywhere, at any time, making it a convenient tool for students, teachers, and professionals.
How to Use an Echelon Form Calculator

Using an echelon form calculator is a straightforward process. Here are the steps involved:
- Enter the matrix: Enter the matrix you want to reduce to its row echelon form. Most online calculators allow you to enter the matrix using a simple input format.
- Select the operation: Select the operation you want to perform, such as reducing the matrix to its row echelon form or solving a system of linear equations.
- Click calculate: Click the calculate button to initiate the calculation.
- View the result: The calculator will display the reduced matrix in its row echelon form.
Steps Involved in Matrix Reduction
Matrix reduction involves a series of row operations to transform the matrix into its row echelon form. Here are the steps involved:
- Swap rows: Swap rows to ensure the leading entry (pivot) is in the top-left corner.
- Multiply rows: Multiply rows by a non-zero constant to ensure the leading entry is equal to 1.
- Add rows: Add rows to eliminate elements below the leading entry.
- Repeat: Repeat the process until the matrix is in its row echelon form.
Practical Applications of Echelon Form Calculators

Echelon form calculators have a range of practical applications in various fields, including:
- Linear algebra: Echelon form calculators are used to solve systems of linear equations, find the inverse of a matrix, and perform other linear algebra operations.
- Engineering: Echelon form calculators are used in engineering to solve systems of linear equations, which is essential for designing and analyzing systems.
- Computer science: Echelon form calculators are used in computer science to solve systems of linear equations, which is essential for machine learning, data analysis, and other applications.
Examples of Echelon Form Calculators in Action
Here are a few examples of echelon form calculators in action:
- Solving a system of linear equations: An echelon form calculator can be used to solve a system of linear equations, such as 2x + 3y = 7 and x - 2y = -3.
- Finding the inverse of a matrix: An echelon form calculator can be used to find the inverse of a matrix, which is essential for solving systems of linear equations.
- Performing matrix operations: An echelon form calculator can be used to perform other matrix operations, such as matrix multiplication and matrix addition.
Conclusion - Take Your Matrix Calculations to the Next Level
Echelon form calculators have revolutionized the way we approach matrix operations, making it easier than ever to perform complex calculations with ease. With their ability to simplify matrix reduction, eliminate human error, and provide accurate results, echelon form calculators are an essential tool for students, teachers, and professionals. Whether you're solving systems of linear equations, finding the inverse of a matrix, or performing other matrix operations, an echelon form calculator is the perfect tool to take your matrix calculations to the next level.
What is the difference between echelon form and reduced row echelon form?
+Echelon form and reduced row echelon form are both simplified forms of a matrix, but they differ in the number of zeros below the leading entry. Echelon form has zeros below the leading entry, while reduced row echelon form has zeros below and above the leading entry.
How do I enter a matrix into an echelon form calculator?
+Most online echelon form calculators allow you to enter the matrix using a simple input format, such as a comma-separated list of numbers.
Can I use an echelon form calculator to solve non-linear equations?
+No, echelon form calculators are designed to solve systems of linear equations. Non-linear equations require different methods and calculators.