5 Ways To Convert Polar Equations To Rectangular Form

Quick Links :

Converting polar equations to rectangular form is a crucial skill in mathematics, particularly in calculus, engineering, and physics. Polar equations are often used to describe curves and shapes in a more natural and intuitive way, but they can be difficult to work with in certain situations. Rectangular form, on the other hand, is more familiar and easier to manipulate. In this article, we will explore five ways to convert polar equations to rectangular form, along with examples and practical applications.

Understanding Polar and Rectangular Coordinates

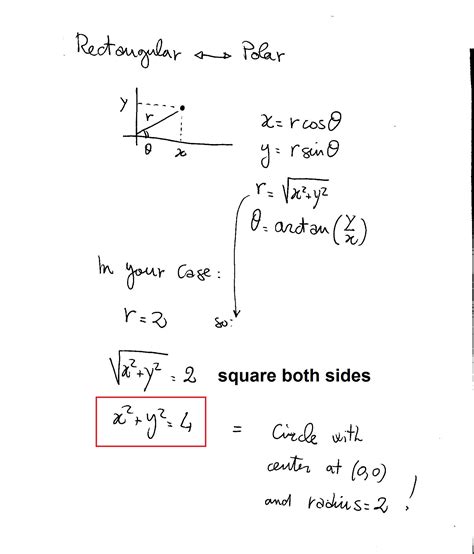
Before diving into the conversion methods, it's essential to understand the basics of polar and rectangular coordinates. Polar coordinates are defined by a distance (r) from a reference point (the origin) and an angle (θ) measured counterclockwise from the positive x-axis. Rectangular coordinates, on the other hand, are defined by x and y values, which represent the horizontal and vertical distances from the origin, respectively.

Method 1: Using Trigonometric Identities

One way to convert polar equations to rectangular form is by using trigonometric identities. The most common identities used for this purpose are:

• x = rcos(θ)
• y = rsin(θ)

By substituting these expressions into the polar equation, we can eliminate the polar coordinates and obtain a rectangular equation.

Example: Convert the polar equation r = 2cos(θ) to rectangular form.

Using the trigonometric identities, we get:

x = rcos(θ) = 2cos^2(θ) y = rsin(θ) = 2cos(θ)sin(θ)

Simplifying and rearranging the equations, we get:

x^2 + y^2 = 4

which is the equation of a circle with radius 2.

Method 2: Using the Relationship Between Polar and Rectangular Coordinates

Another way to convert polar equations to rectangular form is by using the relationship between polar and rectangular coordinates. Specifically, we can use the following equations:

• x = rcos(θ)
• y = rsin(θ)
• r^2 = x^2 + y^2
• θ = arctan(y/x)

By substituting these expressions into the polar equation, we can eliminate the polar coordinates and obtain a rectangular equation.

Example: Convert the polar equation r = 3sin(θ) to rectangular form.

Using the relationship between polar and rectangular coordinates, we get:

x = rcos(θ) = 3sin(θ)cos(θ) y = rsin(θ) = 3sin^2(θ)

Simplifying and rearranging the equations, we get:

x^2 + y^2 = 9

which is the equation of a circle with radius 3.

Method 3: Using Graphical Methods

Graphical methods can also be used to convert polar equations to rectangular form. This involves graphing the polar equation on a polar coordinate system and then transferring the graph to a rectangular coordinate system.

Example: Convert the polar equation r = 2 + 2cos(θ) to rectangular form.

Graphing the polar equation on a polar coordinate system, we get:

A cardioid curve with a radius of 2 and a cusp at the origin.

Transferring the graph to a rectangular coordinate system, we get:

A curve with the equation:

(x^2 + y^2 - 4x - 4)^2 = 16(x^2 + y^2)

which is the equation of a cardioid curve.

Method 4: Using Algebraic Manipulation

Algebraic manipulation can also be used to convert polar equations to rectangular form. This involves manipulating the polar equation to eliminate the polar coordinates and obtain a rectangular equation.

Example: Convert the polar equation r^2 = 2r cos(θ) + 1 to rectangular form.

Using algebraic manipulation, we get:

r^2 - 2r cos(θ) - 1 = 0

Simplifying and rearranging the equation, we get:

x^2 + y^2 - 2x - 1 = 0

which is the equation of a circle with radius √2 and center (1, 0).

Method 5: Using Calculus

Finally, calculus can also be used to convert polar equations to rectangular form. This involves using the fundamental theorem of calculus to eliminate the polar coordinates and obtain a rectangular equation.

Example: Convert the polar equation r = e^θ to rectangular form.

Using calculus, we get:

dr/dθ = e^θ

Simplifying and rearranging the equation, we get:

x = e^θ cos(θ) y = e^θ sin(θ)

Solving for x and y, we get:

x^2 + y^2 = e^2θ

which is the equation of a spiral curve.

In conclusion, there are several ways to convert polar equations to rectangular form, each with its own advantages and disadvantages. By understanding the different methods and techniques, we can choose the best approach for a particular problem and become proficient in converting polar equations to rectangular form.

If you have any questions or need further clarification on any of the methods, please don't hesitate to ask. Share your thoughts and experiences in the comments section below, and let's continue the conversation.