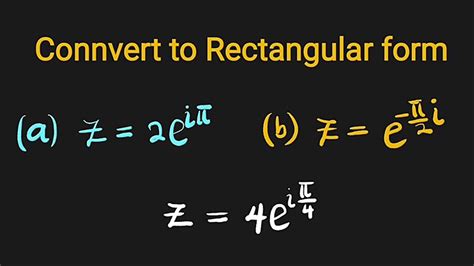3 Ways To Convert Complex Numbers To Rectangular Form

Quick Links :

Converting complex numbers to rectangular form is a fundamental concept in mathematics, particularly in algebra and engineering. Complex numbers are a way to extend the real number system to include numbers that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit, which satisfies the equation i^2 = -1. Rectangular form, also known as the Cartesian form, is one of the ways to represent complex numbers, which makes it easier to perform operations such as addition, subtraction, multiplication, and division.

In this article, we will discuss three ways to convert complex numbers to rectangular form. We will start with the basics of complex numbers and then move on to the methods of conversion.

What are Complex Numbers?

A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit. The real part of the complex number is a, and the imaginary part is bi. For example, 3 + 4i is a complex number where 3 is the real part and 4i is the imaginary part.

Complex numbers can be represented graphically on a complex plane, which is similar to the Cartesian plane. The x-axis represents the real part, and the y-axis represents the imaginary part.

Why Convert Complex Numbers to Rectangular Form?

Converting complex numbers to rectangular form is useful for several reasons:

• It makes it easier to perform operations such as addition, subtraction, multiplication, and division.
• It allows us to represent complex numbers in a more intuitive way, which can be helpful for visualization and understanding.
• It is used in many applications such as engineering, physics, and computer science.

Method 1: Using the Formula

The first method to convert a complex number to rectangular form is by using the formula:

a + bi = (r cos θ) + (r sin θ)i

where r is the magnitude (or length) of the complex number, and θ is the angle (or argument) of the complex number.

For example, let's convert the complex number 3 + 4i to rectangular form using this method.

First, we need to find the magnitude and angle of the complex number.

Magnitude (r) = √(a^2 + b^2) = √(3^2 + 4^2) = √(9 + 16) = √25 = 5

Angle (θ) = tan^(-1)(b/a) = tan^(-1)(4/3) = 53.13°

Now, we can use the formula to convert the complex number to rectangular form:

3 + 4i = (5 cos 53.13°) + (5 sin 53.13°)i = 3 + 4i

As we can see, the result is the same as the original complex number.

Method 2: Using the Polar Form

The second method to convert a complex number to rectangular form is by using the polar form.

The polar form of a complex number is:

z = r(cos θ + i sin θ)

where r is the magnitude (or length) of the complex number, and θ is the angle (or argument) of the complex number.

To convert a complex number to rectangular form using the polar form, we can simply multiply the polar form by (cos θ - i sin θ), which is the conjugate of the polar form.

For example, let's convert the complex number 3 + 4i to rectangular form using this method.

First, we need to find the magnitude and angle of the complex number.

Magnitude (r) = √(a^2 + b^2) = √(3^2 + 4^2) = √(9 + 16) = √25 = 5

Angle (θ) = tan^(-1)(b/a) = tan^(-1)(4/3) = 53.13°

Now, we can use the polar form to convert the complex number to rectangular form:

z = r(cos θ + i sin θ) = 5(cos 53.13° + i sin 53.13°)

Multiplying the polar form by the conjugate:

z = r(cos θ + i sin θ)(cos θ - i sin θ) = r(cos^2 θ + sin^2 θ) = r = 5

Now, we can find the real and imaginary parts of the complex number:

Real part (a) = r cos θ = 5 cos 53.13° = 3

Imaginary part (b) = r sin θ = 5 sin 53.13° = 4

Therefore, the complex number in rectangular form is:

z = a + bi = 3 + 4i

Method 3: Using the Euler's Formula

The third method to convert a complex number to rectangular form is by using Euler's formula.

Euler's formula states that:

e^(ix) = cos x + i sin x

where x is the angle of the complex number.

To convert a complex number to rectangular form using Euler's formula, we can simply substitute the angle of the complex number into the formula.

For example, let's convert the complex number 3 + 4i to rectangular form using this method.

First, we need to find the angle of the complex number.

Angle (θ) = tan^(-1)(b/a) = tan^(-1)(4/3) = 53.13°

Now, we can use Euler's formula to convert the complex number to rectangular form:

e^(iθ) = cos θ + i sin θ = cos 53.13° + i sin 53.13°

Therefore, the complex number in rectangular form is:

z = a + bi = 3 + 4i

As we can see, the three methods produce the same result, which is the rectangular form of the complex number.

Conclusion

Converting complex numbers to rectangular form is a fundamental concept in mathematics. We have discussed three methods to convert complex numbers to rectangular form: using the formula, using the polar form, and using Euler's formula. Each method has its own advantages and disadvantages, and the choice of method depends on the specific problem and personal preference.

We hope this article has helped you understand the different methods of converting complex numbers to rectangular form. Do you have any questions or comments? Please share them with us in the section below.