Unlocking the Secrets of Conic Forms: A Deep Dive into Parabolas

In mathematics, conic forms are a fundamental concept in geometry and algebra. Among these forms, parabolas hold a special place due to their unique properties and applications in various fields. From projectile motion to satellite dishes, parabolas play a crucial role in shaping our understanding of the world. In this article, we will delve into the conic form of a parabola, exploring its definition, equation, and practical applications.
What is a Parabola?
A parabola is a type of conic section, which is a curve obtained by intersecting a cone with a plane. It is defined as the set of all points that are equidistant from a fixed point, known as the focus, and a fixed line, known as the directrix. This unique property makes parabolas useful in modeling various real-world phenomena, such as the trajectory of a thrown ball or the shape of a satellite dish.
The Equation of a Parabola

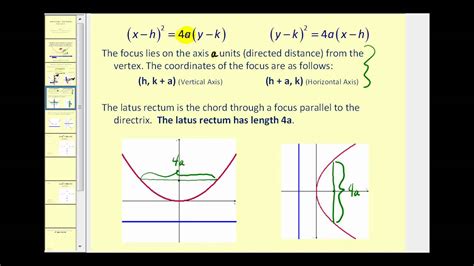
The standard equation of a parabola is given by:
x^2 = 4py
where (x, y) represents a point on the parabola, and p is the distance from the focus to the vertex. The focus is located at the point (0, p), and the directrix is the line y = -p.
Derivation of the Equation
To derive the equation of a parabola, we can start with the definition of a parabola as the set of all points equidistant from the focus and directrix. Let P(x, y) be a point on the parabola, and let F(0, p) be the focus. The distance from P to F is given by:
√(x^2 + (y - p)^2)
The distance from P to the directrix is given by:
|y + p|
Since P is equidistant from F and the directrix, we can set up the equation:
√(x^2 + (y - p)^2) = |y + p|
Simplifying this equation, we get:
x^2 = 4py
which is the standard equation of a parabola.
Properties of Parabolas

Parabolas have several important properties that make them useful in various applications:
- Focus: The focus is the point from which distances are measured in a parabola. It is located at the point (0, p).
- Directrix: The directrix is the line from which distances are measured in a parabola. It is located at the line y = -p.
- Vertex: The vertex is the point at which the parabola intersects its axis of symmetry. It is located at the point (0, 0).
- Axis of Symmetry: The axis of symmetry is the line that passes through the vertex and is perpendicular to the directrix.
Applications of Parabolas
Parabolas have numerous applications in various fields, including:
- Projectile Motion: Parabolas are used to model the trajectory of projectiles, such as thrown balls or launched rockets.
- Optics: Parabolas are used to design mirrors and lenses that focus light to a single point.
- Satellite Dishes: Parabolas are used to design satellite dishes that collect and focus radio waves.
- Architecture: Parabolas are used to design arches and bridges that distribute weight evenly.
Conclusion
In conclusion, the conic form of a parabola is a fundamental concept in mathematics that has numerous applications in various fields. Understanding the equation and properties of parabolas is crucial for modeling and analyzing real-world phenomena. We hope that this article has provided a comprehensive introduction to parabolas and their significance in mathematics and science.
What is the standard equation of a parabola?
+The standard equation of a parabola is x^2 = 4py, where (x, y) represents a point on the parabola, and p is the distance from the focus to the vertex.
What are the properties of parabolas?
+Parabolas have several important properties, including the focus, directrix, vertex, and axis of symmetry.
What are the applications of parabolas?
+Parabolas have numerous applications in various fields, including projectile motion, optics, satellite dishes, and architecture.