Find Resultant Vector In Component Form Easily

Quick Links :

When working with vectors in physics and mathematics, finding the resultant vector in component form can be a challenging task, especially for those who are new to the subject. However, with a clear understanding of the concepts and the right approach, it can be done easily and efficiently. In this article, we will explore the concept of resultant vectors, how to find them in component form, and provide practical examples to help solidify your understanding.

What is a Resultant Vector?

A resultant vector is a vector that results from the combination of two or more vectors. It is the vector that represents the sum of the given vectors. In other words, it is the vector that has the same effect as the individual vectors combined. Resultant vectors are used to simplify complex problems involving multiple vectors and to find the net effect of the vectors.

Why is Finding Resultant Vectors Important?

Finding resultant vectors is crucial in many areas of physics and engineering, such as mechanics, electromagnetism, and civil engineering. It helps to:

• Simplify complex problems involving multiple vectors
• Find the net effect of vectors
• Calculate the magnitude and direction of the resultant vector
• Determine the equilibrium of a system

How to Find Resultant Vectors in Component Form

To find the resultant vector in component form, you need to follow these steps:

1. Break down the vectors into their components: Each vector can be broken down into its x, y, and z components.
2. Add the corresponding components: Add the x components of the vectors, add the y components, and add the z components.
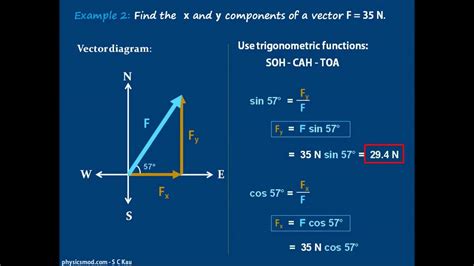
3. Find the magnitude and direction of the resultant vector: Use the Pythagorean theorem to find the magnitude of the resultant vector, and use the inverse tangent function to find its direction.

Example Problem

Find the resultant vector of two vectors A and B, where A = 3i + 4j and B = 2i - 3j.

Step 1: Break down the vectors into their components

A = 3i + 4j B = 2i - 3j

Step 2: Add the corresponding components

Resultant vector = (3 + 2)i + (4 - 3)j = 5i + j

Step 3: Find the magnitude and direction of the resultant vector

Magnitude = √(5^2 + 1^2) = √26 Direction = tan^-1(1/5) = 11.31°

Practical Applications of Resultant Vectors

Resultant vectors have many practical applications in various fields, including:

• Physics and Engineering: Resultant vectors are used to calculate the net force acting on an object, the velocity of an object, and the acceleration of an object.
• Navigation: Resultant vectors are used to determine the direction and magnitude of the resultant velocity of an object.
• Computer Graphics: Resultant vectors are used to calculate the position and orientation of objects in 3D space.

Conclusion

Finding the resultant vector in component form is an essential skill in physics and mathematics. By breaking down the vectors into their components, adding the corresponding components, and finding the magnitude and direction of the resultant vector, you can easily find the resultant vector in component form. With practice and experience, you can apply this skill to solve complex problems involving multiple vectors and to simplify your calculations.