Trigonometric form calculators have become an essential tool for students, engineers, and professionals who work with complex numbers and trigonometry. These calculators help simplify complex calculations, save time, and reduce errors. However, mastering trigonometric form calculators requires practice, patience, and a deep understanding of trigonometric concepts. In this article, we will explore five ways to master trigonometric form calculators and become proficient in using them.

Understanding Trigonometric Concepts
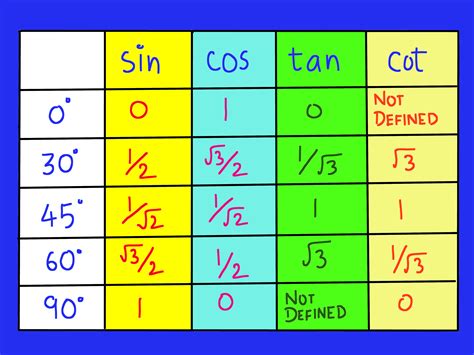
Before mastering trigonometric form calculators, it's essential to have a solid understanding of trigonometric concepts. Trigonometry deals with the relationships between the sides and angles of triangles. It involves the use of trigonometric functions such as sine, cosine, and tangent to describe these relationships. To master trigonometric form calculators, you should be familiar with the following concepts:
- Trigonometric identities: These are equations that involve trigonometric functions and are used to simplify complex expressions.
- Trigonometric functions: These include sine, cosine, tangent, cotangent, secant, and cosecant.
- Polar coordinates: These are used to represent complex numbers in a two-dimensional plane.
- De Moivre's theorem: This theorem provides a formula for raising complex numbers to powers.
Trigonometric Identities
Trigonometric identities are essential for simplifying complex expressions in trigonometric form calculators. Some common trigonometric identities include:
- sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
- cos(a + b) = cos(a)cos(b) - sin(a)sin(b)
- tan(a + b) = (tan(a) + tan(b)) / (1 - tan(a)tan(b))
Practicing with Sample Problems
Practicing with sample problems is an effective way to master trigonometric form calculators. You can find sample problems online or in textbooks that cover trigonometry and complex numbers. Start with simple problems and gradually move on to more complex ones. Make sure to check your answers with a calculator or by working out the problem manually.

Using Online Resources
There are many online resources available that can help you master trigonometric form calculators. Some popular resources include:
- Khan Academy: This website provides video tutorials and practice exercises on trigonometry and complex numbers.
- Wolfram Alpha: This online calculator can simplify complex expressions and solve equations involving trigonometric functions.
- Mathway: This online calculator can solve math problems step-by-step, including trigonometry and complex numbers.
Benefits of Online Resources
Online resources offer several benefits, including:
- Convenience: You can access online resources from anywhere with an internet connection.
- Flexibility: You can learn at your own pace and revisit topics as many times as you need.
- Interactivity: Many online resources provide interactive tutorials and practice exercises that make learning more engaging.
Mastering Polar Coordinates
Polar coordinates are used to represent complex numbers in a two-dimensional plane. To master trigonometric form calculators, you need to understand how to convert between polar and rectangular coordinates. Some key concepts to understand include:
- Polar coordinates: These are used to represent complex numbers in the form (r, θ), where r is the radius and θ is the angle.
- Rectangular coordinates: These are used to represent complex numbers in the form (x, y), where x is the real part and y is the imaginary part.

De Moivre's Theorem
De Moivre's theorem provides a formula for raising complex numbers to powers. To master trigonometric form calculators, you need to understand how to apply De Moivre's theorem to simplify complex expressions. Some key concepts to understand include:
- De Moivre's theorem: This theorem states that (cos(x) + i sin(x))^n = cos(nx) + i sin(nx).
- Applications: De Moivre's theorem can be used to simplify complex expressions involving powers of complex numbers.
Example Problem
Find the value of (cos(30°) + i sin(30°))^3.
Solution: Using De Moivre's theorem, we can simplify the expression as follows:
(cos(30°) + i sin(30°))^3 = cos(3 × 30°) + i sin(3 × 30°) = cos(90°) + i sin(90°) = 0 + i
Conclusion
Mastering trigonometric form calculators requires practice, patience, and a deep understanding of trigonometric concepts. By understanding trigonometric identities, practicing with sample problems, using online resources, mastering polar coordinates, and applying De Moivre's theorem, you can become proficient in using trigonometric form calculators. Remember to start with simple problems and gradually move on to more complex ones, and don't hesitate to seek help when needed.

What is a trigonometric form calculator?
+A trigonometric form calculator is a tool used to simplify complex expressions involving trigonometric functions and complex numbers.
What are the benefits of using online resources to master trigonometric form calculators?
+Online resources offer convenience, flexibility, and interactivity, making it easier to learn and master trigonometric form calculators.
How do I apply De Moivre's theorem to simplify complex expressions?
+De Moivre's theorem provides a formula for raising complex numbers to powers. To apply it, simply raise the complex number to the power using the formula (cos(x) + i sin(x))^n = cos(nx) + i sin(nx).