Vectors are a fundamental concept in mathematics and physics, used to represent quantities with both magnitude and direction. In many applications, it's essential to find the component form of a vector, which involves breaking down the vector into its constituent parts along the x, y, and z axes. In this article, we'll explore the concept of component form of a vector calculator using magnitude and direction.
Understanding Vectors and Their Component Form

A vector is a mathematical object that has both magnitude (length) and direction. It can be represented graphically as an arrow in a coordinate system. The component form of a vector is a way of expressing the vector in terms of its projections along the x, y, and z axes. This is useful in many applications, such as physics, engineering, and computer science.
Why is Component Form Important?
The component form of a vector is essential in many areas, including:
- Physics: to describe the motion of objects in two or three dimensions
- Engineering: to calculate forces, stresses, and strains in complex systems
- Computer Science: to perform tasks such as computer graphics, game development, and scientific simulations
Calculating the Component Form of a Vector

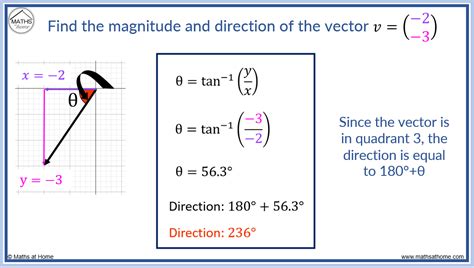
To calculate the component form of a vector, you need to know the magnitude (length) and direction of the vector. The direction is usually specified in terms of the angle the vector makes with the x-axis. The component form of a vector can be calculated using the following formulas:
- x-component: Vx = |V| * cos(θ)
- y-component: Vy = |V| * sin(θ)
- z-component: Vz = |V| * cos(φ)
where |V| is the magnitude of the vector, θ is the angle with the x-axis, and φ is the angle with the z-axis.
Using a Component Form of a Vector Calculator
There are many online calculators available that can help you calculate the component form of a vector. These calculators typically require you to input the magnitude and direction of the vector, and then output the x, y, and z components of the vector.
Example Problems

Here are some example problems to illustrate the concept of component form of a vector:
- Problem 1: Find the component form of a vector with magnitude 5 units and direction 30° with the x-axis.
- Problem 2: Calculate the component form of a vector with magnitude 10 units and direction 45° with the x-axis.
- Problem 3: Find the component form of a vector with magnitude 7 units and direction 60° with the x-axis.
Solutions to Example Problems
- Problem 1:
- x-component: Vx = 5 * cos(30°) = 4.33
- y-component: Vy = 5 * sin(30°) = 2.5
- Problem 2:
- x-component: Vx = 10 * cos(45°) = 7.07
- y-component: Vy = 10 * sin(45°) = 7.07
- Problem 3:
- x-component: Vx = 7 * cos(60°) = 3.5
- y-component: Vy = 7 * sin(60°) = 6.06
Real-World Applications

The component form of a vector has many real-world applications, including:
- Physics: to describe the motion of objects in two or three dimensions
- Engineering: to calculate forces, stresses, and strains in complex systems
- Computer Science: to perform tasks such as computer graphics, game development, and scientific simulations
Conclusion
In conclusion, the component form of a vector is a fundamental concept in mathematics and physics, used to break down a vector into its constituent parts along the x, y, and z axes. Calculating the component form of a vector requires knowledge of the magnitude and direction of the vector, and can be performed using online calculators or manual calculations. The component form of a vector has many real-world applications, including physics, engineering, and computer science.
What is the component form of a vector?
+The component form of a vector is a way of expressing the vector in terms of its projections along the x, y, and z axes.
How do I calculate the component form of a vector?
+To calculate the component form of a vector, you need to know the magnitude (length) and direction of the vector. The direction is usually specified in terms of the angle the vector makes with the x-axis.
What are some real-world applications of the component form of a vector?
+The component form of a vector has many real-world applications, including physics, engineering, and computer science.