Rewrite Polynomial In Standard Form Made Easy

Quick Links :

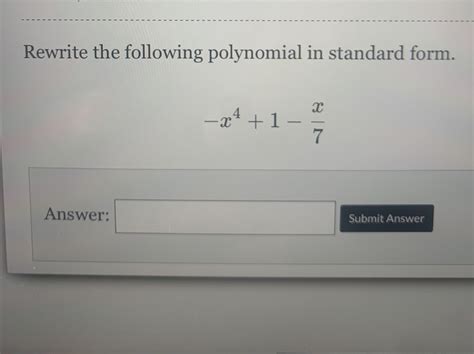
Polynomial expressions are a fundamental concept in algebra, and understanding how to rewrite them in standard form is a crucial skill for students to master. In this article, we will explore the concept of polynomial expressions, the importance of standard form, and provide a step-by-step guide on how to rewrite polynomials in standard form.

The Importance of Polynomial Expressions

Polynomial expressions are used to describe a wide range of phenomena in mathematics, science, and engineering. They are a powerful tool for modeling complex relationships and solving problems. Polynomial expressions consist of variables, coefficients, and exponents, and they can be combined using basic arithmetic operations.

One of the key benefits of polynomial expressions is that they can be easily manipulated and simplified. However, this simplification process requires that the polynomial be in standard form. Standard form is a specific way of writing a polynomial expression, and it is essential for many mathematical operations, such as adding, subtracting, and multiplying polynomials.

What is Standard Form?

Standard form is a way of writing a polynomial expression in which the terms are arranged in descending order of exponents. For example, the polynomial expression 3x^2 + 2x - 4 is in standard form because the terms are arranged in descending order of exponents. The first term has the highest exponent, and the last term has the lowest exponent.

The Benefits of Standard Form

There are several benefits to writing polynomial expressions in standard form. One of the main advantages is that it makes it easier to compare and combine polynomial expressions. When polynomials are in standard form, it is easy to see which terms have the same exponent, making it simpler to add and subtract them.

Standard form also makes it easier to identify the degree of a polynomial. The degree of a polynomial is the highest exponent of any term in the polynomial. By writing a polynomial in standard form, you can easily identify the degree of the polynomial.

How to Rewrite Polynomials in Standard Form

Rewriting a polynomial expression in standard form involves rearranging the terms in descending order of exponents. Here are the steps to follow:

1. Identify the terms: Start by identifying the individual terms in the polynomial expression. A term is a single part of the polynomial that is separated from the other parts by a plus or minus sign.
2. Determine the exponents: Next, determine the exponent of each term. The exponent is the power to which the variable is raised.
3. Arrange the terms: Arrange the terms in descending order of exponents. Start with the term that has the highest exponent and end with the term that has the lowest exponent.
4. Combine like terms: Finally, combine any like terms. Like terms are terms that have the same exponent.

Examples of Rewriting Polynomials in Standard Form

Let's look at a few examples of rewriting polynomial expressions in standard form.

Example 1

Suppose we have the polynomial expression 2x^3 + 4x^2 - 3x + 1. To rewrite this expression in standard form, we need to arrange the terms in descending order of exponents.

• 2x^3 has an exponent of 3
• 4x^2 has an exponent of 2
• -3x has an exponent of 1
• 1 has an exponent of 0

In descending order of exponents, the terms are: 2x^3, 4x^2, -3x, 1.

The polynomial expression in standard form is: 2x^3 + 4x^2 - 3x + 1

Example 2

Suppose we have the polynomial expression x^2 - 4x + 3x^3 - 2. To rewrite this expression in standard form, we need to arrange the terms in descending order of exponents.

• 3x^3 has an exponent of 3
• x^2 has an exponent of 2
• -4x has an exponent of 1
• 3x has an exponent of 1
• -2 has an exponent of 0

In descending order of exponents, the terms are: 3x^3, x^2, -4x + 3x, -2.

Combining the like terms -4x and 3x, we get -x.

The polynomial expression in standard form is: 3x^3 + x^2 - x - 2

Tips and Tricks

Here are a few tips and tricks to keep in mind when rewriting polynomial expressions in standard form:

• Always arrange the terms in descending order of exponents.
• Combine like terms to simplify the expression.
• Use the distributive property to expand and simplify expressions.
• Check your work by plugging in values for the variables and evaluating the expression.

Conclusion

Rewriting polynomial expressions in standard form is an essential skill in algebra. By following the steps outlined in this article, you can easily rewrite polynomial expressions in standard form. Remember to always arrange the terms in descending order of exponents, combine like terms, and use the distributive property to expand and simplify expressions.

We hope this article has been helpful in explaining the concept of polynomial expressions and how to rewrite them in standard form. If you have any questions or need further clarification, please don't hesitate to ask.