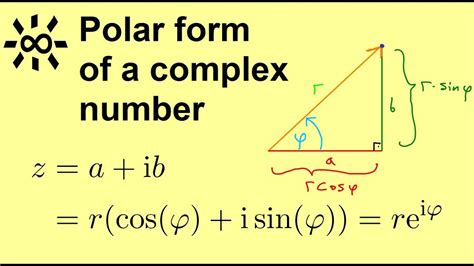Polar form, a mathematical concept that has been a cornerstone of algebra and trigonometry for centuries. While it's a powerful tool for representing complex numbers, the formula can be intimidating, especially for those who are new to the subject. In this article, we'll explore five ways to simplify the polar form formula, making it more accessible and easier to understand.
What is Polar Form?

Polar form is a way of representing complex numbers in terms of their magnitude (or length) and direction. It's a convenient way to express complex numbers in trigonometric form, making it easier to perform operations like multiplication and division. The polar form formula is:
z = r(cosθ + isinθ)
where z is the complex number, r is the magnitude, θ is the angle, and i is the imaginary unit.
1. Understand the Concept of Magnitude and Direction

The first step to simplifying the polar form formula is to understand the concept of magnitude and direction. The magnitude (or length) of a complex number represents its distance from the origin in the complex plane. The direction, on the other hand, represents the angle at which the complex number is measured from the positive real axis.
Think of it like a vector in a coordinate plane. The magnitude is the length of the vector, while the direction is the angle at which it's pointing. Once you grasp this concept, you'll find it easier to work with the polar form formula.
Example:
Find the magnitude and direction of the complex number z = 3 + 4i.
Magnitude (r) = √(3² + 4²) = √(9 + 16) = √25 = 5 Direction (θ) = arctan(4/3) ≈ 53.13°
2. Use the Pythagorean Theorem to Find the Magnitude

Another way to simplify the polar form formula is to use the Pythagorean theorem to find the magnitude. The Pythagorean theorem states that the square of the hypotenuse (the magnitude) is equal to the sum of the squares of the other two sides.
r² = x² + y²
where x and y are the real and imaginary parts of the complex number, respectively.
Example:
Find the magnitude of the complex number z = 2 + 3i using the Pythagorean theorem.
r² = 2² + 3² = 4 + 9 = 13 r = √13 ≈ 3.61
3. Convert Rectangular Form to Polar Form

Converting rectangular form to polar form is another way to simplify the polar form formula. Rectangular form represents complex numbers in terms of their real and imaginary parts, while polar form represents them in terms of their magnitude and direction.
To convert rectangular form to polar form, use the following formulas:
r = √(x² + y²) θ = arctan(y/x)
where x and y are the real and imaginary parts of the complex number, respectively.
Example:
Convert the complex number z = 2 + 3i from rectangular form to polar form.
r = √(2² + 3²) = √13 ≈ 3.61 θ = arctan(3/2) ≈ 56.31°
4. Use Trigonometric Identities to Simplify the Formula

Trigonometric identities can be used to simplify the polar form formula. One common identity is the double-angle formula for sine and cosine:
cos(2θ) = cos²θ - sin²θ sin(2θ) = 2sinθcosθ
These identities can be used to simplify the polar form formula by combining the sine and cosine terms.
Example:
Simplify the polar form formula using the double-angle formula for sine and cosine.
z = r(cosθ + isinθ) = r(cos(2θ) + isin(2θ)) = r((cos²θ - sin²θ) + i(2sinθcosθ))
5. Practice, Practice, Practice!

Finally, the best way to simplify the polar form formula is to practice, practice, practice! The more you work with the formula, the more comfortable you'll become with its structure and syntax.
Try simplifying different complex numbers using the formulas and techniques outlined above. The more you practice, the easier it will become to work with the polar form formula.
What is the polar form formula?
+The polar form formula is z = r(cosθ + isinθ), where z is the complex number, r is the magnitude, θ is the angle, and i is the imaginary unit.
How do I find the magnitude of a complex number?
+The magnitude of a complex number can be found using the Pythagorean theorem: r² = x² + y², where x and y are the real and imaginary parts of the complex number, respectively.
Can I simplify the polar form formula using trigonometric identities?
+In conclusion, simplifying the polar form formula requires a combination of understanding the concept of magnitude and direction, using the Pythagorean theorem, converting rectangular form to polar form, using trigonometric identities, and practicing, practicing, practicing! By following these tips and techniques, you'll become more comfortable working with the polar form formula and be able to simplify it with ease.
We hope this article has been helpful in your journey to simplify the polar form formula. If you have any questions or need further clarification, please don't hesitate to ask. Share your thoughts and comments below, and don't forget to share this article with your friends and colleagues who may find it helpful.