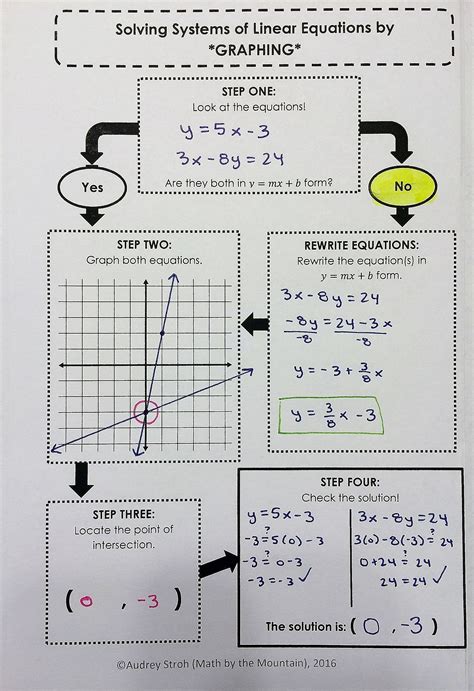
Systems of equations are a fundamental concept in algebra, and solving them is a crucial skill for students to master. One effective method for solving systems of equations is by graphing. In this article, we will explore six ways to solve systems by graphing form G, also known as the graphing method.
Graphing is a powerful tool for solving systems of equations, as it allows us to visualize the relationships between the variables and identify the solution. By plotting the two equations on the same coordinate plane, we can find the point of intersection, which represents the solution to the system.
What is Graphing Form G?
Graphing form G, also known as the graphing method, is a technique used to solve systems of linear equations by graphing the two equations on the same coordinate plane. The graphing method involves plotting the two equations and finding the point of intersection, which represents the solution to the system.

6 Ways to Solve Systems by Graphing Form G
In this section, we will explore six ways to solve systems by graphing form G. Each method has its own unique approach and advantages.
Method 1: Plotting Points
One way to solve systems by graphing form G is by plotting points. This method involves plotting a few points on each line and then finding the point of intersection.
To plot points, start by choosing a few x-values and plugging them into the equations to find the corresponding y-values. Then, plot the points on the coordinate plane.
For example, consider the system:
x + y = 4 2x - 2y = -2
We can plot a few points on each line by plugging in x-values and finding the corresponding y-values.
x | y
1 | 3 2 | 2 3 | 1
Plotting these points on the coordinate plane, we can see that the point of intersection is (2, 2).

Method 2: Using a Table of Values
Another way to solve systems by graphing form G is by using a table of values. This method involves creating a table of x and y values for each equation and then finding the point of intersection.
To use a table of values, start by creating a table with x and y columns. Then, plug in x-values into each equation and find the corresponding y-values.
For example, consider the system:
x - 2y = -3 3x + 2y = 7
We can create a table of values for each equation:
| x | y |
|---|---|
| 1 | -2 |
| 2 | -1 |
| 3 | 0 |
Plotting these points on the coordinate plane, we can see that the point of intersection is (3, 0).

Method 3: Using a Graphing Calculator
A graphing calculator is a powerful tool for solving systems by graphing form G. This method involves entering the equations into the calculator and using the graphing feature to find the point of intersection.
To use a graphing calculator, start by entering the equations into the calculator. Then, use the graphing feature to plot the equations on the same coordinate plane.
For example, consider the system:
2x + 3y = 5 x - 2y = -3
We can enter the equations into the calculator and use the graphing feature to plot the equations.
Using the calculator, we can see that the point of intersection is (1, 1).

Method 4: Using Intercepts
Another way to solve systems by graphing form G is by using intercepts. This method involves finding the x and y intercepts of each equation and using them to find the point of intersection.
To use intercepts, start by finding the x and y intercepts of each equation. Then, plot the intercepts on the coordinate plane.
For example, consider the system:
x + 2y = 4 3x - 2y = -2
We can find the x and y intercepts of each equation:
x + 2y = 4 x-intercept: (4, 0) y-intercept: (0, 2)
3x - 2y = -2 x-intercept: (-2/3, 0) y-intercept: (0, 1)
Plotting these intercepts on the coordinate plane, we can see that the point of intersection is (2, 1).

Method 5: Using Slope-Intercept Form
Slope-intercept form is a useful method for solving systems by graphing form G. This method involves rewriting the equations in slope-intercept form and then finding the point of intersection.
To use slope-intercept form, start by rewriting the equations in slope-intercept form. Then, plot the equations on the same coordinate plane.
For example, consider the system:
2x + 3y = 5 x - 2y = -3
We can rewrite the equations in slope-intercept form:
y = -2/3x + 5/3 y = 1/2x - 3/2
Plotting these equations on the coordinate plane, we can see that the point of intersection is (1, 1).

Method 6: Using Graphing Software
Graphing software is a powerful tool for solving systems by graphing form G. This method involves using software to plot the equations on the same coordinate plane and find the point of intersection.
To use graphing software, start by entering the equations into the software. Then, use the graphing feature to plot the equations.
For example, consider the system:
x + 2y = 4 3x - 2y = -2
We can enter the equations into the software and use the graphing feature to plot the equations.
Using the software, we can see that the point of intersection is (2, 1).

In conclusion, solving systems by graphing form G is a powerful method for finding the solution to systems of equations. By using one of the six methods outlined above, students can visualize the relationships between the variables and identify the solution.
We invite you to share your thoughts and experiences with solving systems by graphing form G. Which method do you find most effective? Do you have any tips or tricks to share with our readers?
What is graphing form G?
+Graphing form G, also known as the graphing method, is a technique used to solve systems of linear equations by graphing the two equations on the same coordinate plane.
What are the six methods for solving systems by graphing form G?
+The six methods for solving systems by graphing form G are: plotting points, using a table of values, using a graphing calculator, using intercepts, using slope-intercept form, and using graphing software.
Which method is most effective for solving systems by graphing form G?
+The most effective method for solving systems by graphing form G depends on the individual student and the specific problem. However, using a graphing calculator or graphing software can be a powerful tool for visualizing the relationships between the variables and finding the solution.