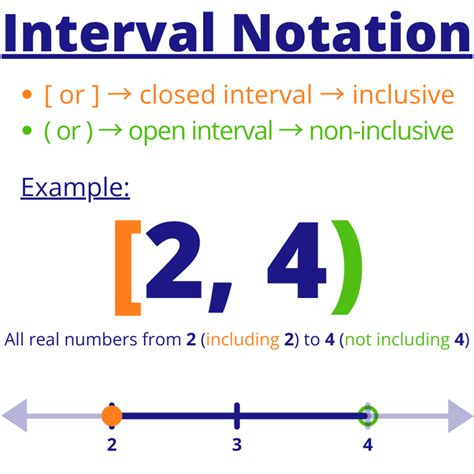
Interval form domain is a fundamental concept in mathematics, particularly in real analysis and calculus. It refers to the way we represent and work with intervals, which are sets of real numbers that can be used to define limits, integrals, and other mathematical operations.
In simple terms, an interval is a set of real numbers that includes all the numbers between two given numbers, called the endpoints. Intervals can be open, closed, or half-open, depending on whether the endpoints are included or excluded. Understanding interval form domain is crucial in various mathematical contexts, including function theory, optimization, and mathematical modeling.
Here, we'll delve into the world of interval form domain, exploring its definition, types, and applications. We'll also discuss the importance of interval notation and provide examples to illustrate the concept.
What is Interval Form Domain?

Interval form domain refers to the way we represent intervals using mathematical notation. An interval is denoted by its endpoints, which can be real numbers or infinity. The notation used to represent an interval depends on whether the endpoints are included or excluded.
For example, the interval [a, b] represents all real numbers x such that a ≤ x ≤ b. This is called a closed interval because it includes both endpoints. On the other hand, the interval (a, b) represents all real numbers x such that a < x < b. This is called an open interval because it excludes both endpoints.
Types of Intervals
There are several types of intervals, each with its own notation and characteristics. Here are some of the most common types of intervals:
- Open interval: (a, b) - excludes both endpoints
- Closed interval: [a, b] - includes both endpoints
- Half-open interval: (a, b] or [a, b) - includes one endpoint and excludes the other
- Infinite interval: (a, ∞) or (-∞, b) - extends to infinity in one direction
- Empty interval: ∅ - contains no elements
Applications of Interval Form Domain

Interval form domain has numerous applications in mathematics and other fields. Here are some examples:
- Function theory: Intervals are used to define the domain and range of functions. Understanding interval notation is essential for working with functions and determining their properties.
- Optimization: Intervals are used to model real-world problems in optimization, such as finding the maximum or minimum value of a function.
- Mathematical modeling: Intervals are used to represent uncertainty or imprecision in mathematical models.
- Calculus: Intervals are used to define limits, integrals, and other fundamental concepts in calculus.
Importance of Interval Notation
Interval notation is a crucial aspect of interval form domain. It provides a concise and unambiguous way to represent intervals, making it easier to work with mathematical expressions and functions. Here are some reasons why interval notation is important:
- Clarity: Interval notation helps to avoid ambiguity and ensures that mathematical expressions are clearly defined.
- Precision: Interval notation allows for precise definition of intervals, which is essential for working with mathematical concepts.
- Efficiency: Interval notation saves time and effort by providing a concise way to represent intervals.
Examples of Interval Form Domain

Here are some examples of interval form domain:
- Open interval: The interval (2, 5) represents all real numbers x such that 2 < x < 5.
- Closed interval: The interval [1, 3] represents all real numbers x such that 1 ≤ x ≤ 3.
- Half-open interval: The interval (4, 6] represents all real numbers x such that 4 < x ≤ 6.
In conclusion, interval form domain is a fundamental concept in mathematics that provides a way to represent and work with intervals. Understanding interval notation and the different types of intervals is crucial for working with mathematical concepts and solving real-world problems. We hope this article has provided a comprehensive overview of interval form domain and its applications.
Call to Action: Share your thoughts on interval form domain and its applications in the comments below. How have you used interval notation in your mathematical endeavors? Do you have any questions or topics you'd like to discuss further?