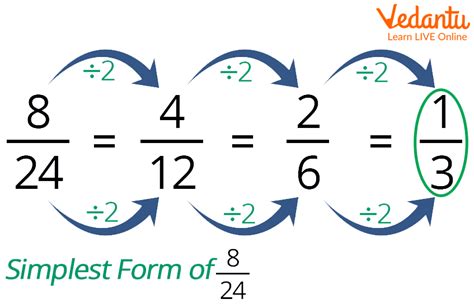
The decimal 0.6 can be converted to a fraction in its simplest form as follows:
0.6 = 6/10
To simplify this fraction, we can divide both the numerator and the denominator by 2, which gives us:
0.6 = 3/5
So, the fraction 3/5 is the simplest form of the decimal 0.6.
Understanding Decimals and Fractions
Decimals and fractions are two different ways of representing numbers. Decimals are a way of expressing numbers using a point (.) to separate the whole part from the fractional part. Fractions, on the other hand, represent numbers as a ratio of two integers, with the top number (numerator) representing the part and the bottom number (denominator) representing the whole.

Converting Decimals to Fractions
Converting decimals to fractions is a useful skill in mathematics. To convert a decimal to a fraction, we can use the following steps:
- Write the decimal as a fraction with the decimal part as the numerator and the place value of the last digit as the denominator.
- Simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD).
For example, the decimal 0.6 can be converted to a fraction as follows:
0.6 = 6/10
The GCD of 6 and 10 is 2, so we can divide both the numerator and the denominator by 2 to simplify the fraction:
0.6 = 3/5
Benefits of Converting Decimals to Fractions
Converting decimals to fractions has several benefits. Here are a few:
- Improved understanding: Fractions can help us understand the underlying structure of numbers and how they relate to each other.
- Simplification: Fractions can be simplified to their lowest terms, making it easier to work with them.
- Flexibility: Fractions can be added, subtracted, multiplied, and divided, making them a versatile tool for mathematical operations.

Real-World Applications of Fractions
Fractions have numerous real-world applications. Here are a few examples:
- Cooking: Recipes often use fractions to specify ingredient quantities. For example, a recipe might call for 3/4 cup of flour.
- Music: Fractions are used in music to represent rhythms and time signatures. For example, a 3/4 time signature indicates that there are three beats in a measure.
- Science: Fractions are used in science to represent proportions and ratios. For example, a scientist might use the fraction 2/3 to represent the proportion of a substance in a mixture.
Common Fractions and Their Decimal Equivalents
Here are some common fractions and their decimal equivalents:
| Fraction | Decimal Equivalent |
|---|---|
| 1/2 | 0.5 |
| 1/3 | 0.33 |
| 2/3 | 0.67 |
| 1/4 | 0.25 |
| 3/4 | 0.75 |

Practice Converting Decimals to Fractions
Now that you know how to convert decimals to fractions, practice converting the following decimals to fractions:
- 0.4
- 0.7
- 0.9
- 0.2
Remember to simplify your fractions to their lowest terms.

Encourage readers to try converting decimals to fractions on their own and to share their experiences in the comments below. Share this article with others who may find it helpful.
FAQ:
What is the simplest form of the fraction 6/10?
+The simplest form of the fraction 6/10 is 3/5.
How do you convert a decimal to a fraction?
+To convert a decimal to a fraction, write the decimal as a fraction with the decimal part as the numerator and the place value of the last digit as the denominator. Then simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD).
What are some real-world applications of fractions?
+Fractions have numerous real-world applications, including cooking, music, and science.