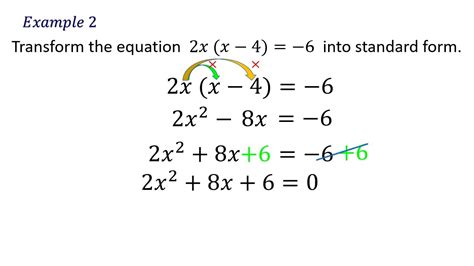5 Ways To Put A Quadratic Equation Into Standard Form

Quick Links :

Quadratic equations are a fundamental concept in algebra, and being able to express them in standard form is a crucial skill for problem-solving. In this article, we will explore five ways to put a quadratic equation into standard form, along with practical examples and explanations to help you master this technique.

What is Standard Form?

The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants, and a cannot be equal to zero. This form is useful for solving quadratic equations using various methods, such as factoring, completing the square, and the quadratic formula.

Method 1: Rearranging the Equation

One of the simplest ways to put a quadratic equation into standard form is to rearrange the terms. For example, consider the equation x^2 + 5 = 3x. To rewrite this equation in standard form, we need to move the term 3x to the left-hand side and simplify.

x^2 - 3x + 5 = 0

By rearranging the terms, we have successfully put the equation into standard form.

Example 1:

Rewrite the equation 2x^2 + 4 = 5x in standard form.

Solution:

2x^2 - 5x + 4 = 0

Method 2: Combining Like Terms

Another way to put a quadratic equation into standard form is to combine like terms. For instance, consider the equation x^2 + 2x + 3x + 1 = 0. We can combine the like terms 2x and 3x to simplify the equation.

x^2 + 5x + 1 = 0

By combining like terms, we have successfully put the equation into standard form.

Example 2:

Rewrite the equation x^2 + 2x - 3x - 4 = 0 in standard form.

Solution:

x^2 - x - 4 = 0

Method 3: Factoring Out the Greatest Common Factor

Factoring out the greatest common factor (GCF) is a useful technique for putting a quadratic equation into standard form. For example, consider the equation 2x^2 + 6x + 4 = 0. We can factor out the GCF, which is 2.

2(x^2 + 3x + 2) = 0

x^2 + 3x + 2 = 0

By factoring out the GCF, we have successfully put the equation into standard form.

Example 3:

Rewrite the equation 3x^2 + 9x + 6 = 0 in standard form.

Solution:

3(x^2 + 3x + 2) = 0

x^2 + 3x + 2 = 0

Method 4: Using the Distributive Property

The distributive property can be used to put a quadratic equation into standard form. For example, consider the equation x^2 + (2 + 3)x + 1 = 0. We can use the distributive property to simplify the equation.

x^2 + 5x + 1 = 0

By using the distributive property, we have successfully put the equation into standard form.

Example 4:

Rewrite the equation x^2 + (4 - 1)x - 3 = 0 in standard form.

Solution:

x^2 + 3x - 3 = 0

Method 5: Using Algebraic Manipulation

Algebraic manipulation can be used to put a quadratic equation into standard form. For example, consider the equation x^2 + 2x = 3x + 1. We can add or subtract terms to both sides of the equation to simplify it.

x^2 - x - 1 = 0

By using algebraic manipulation, we have successfully put the equation into standard form.

Example 5:

Rewrite the equation x^2 + 3x = 2x + 4 in standard form.

Solution:

x^2 + x - 4 = 0

In conclusion, putting a quadratic equation into standard form is an essential skill for problem-solving in algebra. By using the five methods outlined above, you can rewrite any quadratic equation in the standard form ax^2 + bx + c = 0. Practice these techniques to become proficient in rewriting quadratic equations.

Now it's your turn! Take a few minutes to practice rewriting quadratic equations in standard form using the methods outlined above. Share your examples in the comments below, and don't hesitate to ask if you have any questions.