Master 4 Essential Skills For Graphing Slope Intercept Form

Quick Links :

Understanding Slope Intercept Form: The Key to Mastering Graphing

Graphing slope intercept form is a fundamental concept in algebra and mathematics. It is used to represent linear equations in a graphical format, making it easier to visualize and analyze relationships between variables. Mastering slope intercept form requires a strong understanding of four essential skills: identifying slope and y-intercept, writing equations in slope intercept form, graphing linear equations, and applying real-world applications.

Skill 1: Identifying Slope and Y-Intercept

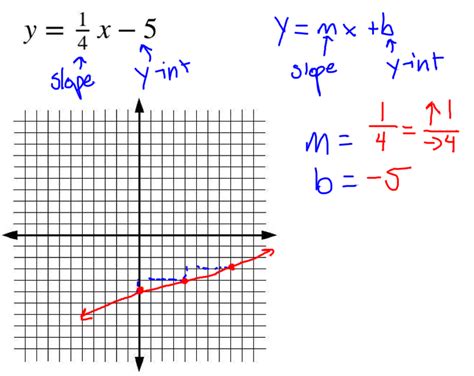
The slope-intercept form of a linear equation is y = mx + b, where m represents the slope and b represents the y-intercept. The slope (m) is a measure of how steep the line is, while the y-intercept (b) is the point where the line crosses the y-axis. To identify the slope and y-intercept, you need to understand the following:

• The slope (m) can be positive, negative, or zero. A positive slope indicates a line that slopes upward from left to right, while a negative slope indicates a line that slopes downward from left to right. A zero slope indicates a horizontal line.
• The y-intercept (b) can be any real number. It represents the point where the line crosses the y-axis.

How to Identify Slope and Y-Intercept

To identify the slope and y-intercept, follow these steps:

1. Write the equation in slope-intercept form (y = mx + b).
2. Identify the coefficient of x, which represents the slope (m).
3. Identify the constant term, which represents the y-intercept (b).

For example, consider the equation y = 2x + 3. In this equation, the slope (m) is 2, and the y-intercept (b) is 3.

Skill 2: Writing Equations in Slope Intercept Form

Writing equations in slope-intercept form requires a strong understanding of algebraic manipulations. To write an equation in slope-intercept form, follow these steps:

1. Write the equation in standard form (Ax + By = C).
2. Add or subtract the same value to both sides of the equation to isolate the term with the variable (x or y).
3. Divide both sides of the equation by the coefficient of the variable to solve for the variable.

For example, consider the equation 2x + 3y = 7. To write this equation in slope-intercept form, follow these steps:

1. Add 3y to both sides of the equation: 2x = -3y + 7.
2. Divide both sides of the equation by 2: x = (-3/2)y + 7/2.
3. Rearrange the equation to isolate y: y = (-2/3)x + 7/3.

The equation is now in slope-intercept form: y = (-2/3)x + 7/3.

Skill 3: Graphing Linear Equations

Graphing linear equations in slope-intercept form requires a strong understanding of coordinate geometry. To graph a linear equation, follow these steps:

1. Identify the slope (m) and y-intercept (b).
2. Plot the y-intercept (b) on the y-axis.
3. Use the slope (m) to plot additional points on the graph.
4. Draw a line through the points to represent the graph of the equation.

For example, consider the equation y = 2x + 3. To graph this equation, follow these steps:

1. Identify the slope (m) and y-intercept (b): m = 2, b = 3.
2. Plot the y-intercept (b) on the y-axis: (0, 3).
3. Use the slope (m) to plot additional points on the graph: (1, 5), (2, 7), (3, 9).
4. Draw a line through the points to represent the graph of the equation.

Skill 4: Applying Real-World Applications

Slope-intercept form has numerous real-world applications, including physics, engineering, economics, and computer science. To apply slope-intercept form to real-world problems, follow these steps:

1. Identify the problem and the variables involved.
2. Write an equation in slope-intercept form to model the problem.
3. Use the equation to make predictions or solve problems.

For example, consider a problem involving a car traveling at a constant speed. The distance traveled (d) is related to the time traveled (t) by the equation d = 60t + 10. To apply this equation to a real-world problem, follow these steps:

1. Identify the problem and the variables involved: d = distance traveled, t = time traveled.
2. Write the equation in slope-intercept form: d = 60t + 10.
3. Use the equation to make predictions or solve problems: If the car travels for 2 hours, how far will it have traveled? d = 60(2) + 10 = 130 miles.

In conclusion, mastering slope-intercept form requires a strong understanding of four essential skills: identifying slope and y-intercept, writing equations in slope-intercept form, graphing linear equations, and applying real-world applications. By practicing these skills, you can become proficient in graphing slope intercept form and apply it to a wide range of problems in mathematics and real-world applications.