Find Focus Of Parabola In Standard Form Easily

Quick Links :

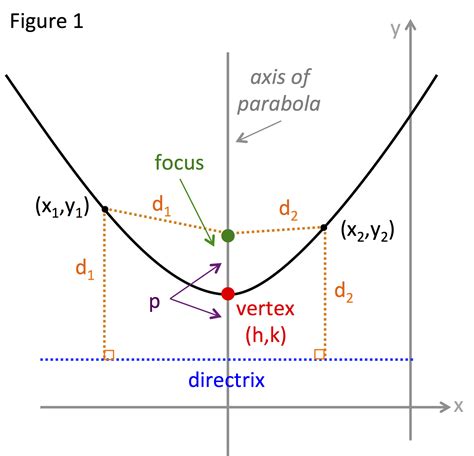
The focus of a parabola is a fixed point that is equidistant from a point on the parabola and the directrix. In this article, we will explore how to find the focus of a parabola in standard form easily.

Parabolas are fascinating curves that are commonly used in various fields, including physics, engineering, and mathematics. One of the key characteristics of a parabola is its focus, which plays a crucial role in understanding the behavior of the curve. In this article, we will delve into the world of parabolas and provide a step-by-step guide on how to find the focus of a parabola in standard form.

What is a Parabola in Standard Form?

A parabola in standard form is represented by the equation y = ax^2 + bx + c, where a, b, and c are constants, and x and y are variables. The standard form of a parabola is also known as the vertex form, which provides valuable information about the parabola's shape, size, and position.

Key Components of a Parabola in Standard Form

Before we dive into finding the focus of a parabola, let's review the key components of a parabola in standard form:

• Vertex (h, k): The vertex is the lowest or highest point on the parabola, depending on the direction of the curve.
• Axis of symmetry: The axis of symmetry is a vertical line that passes through the vertex and is equidistant from the two sides of the parabola.
• Focus (p, q): The focus is a fixed point that is equidistant from a point on the parabola and the directrix.
• Directrix: The directrix is a horizontal line that is perpendicular to the axis of symmetry and is used to define the parabola.

How to Find the Focus of a Parabola in Standard Form

Now that we have reviewed the key components of a parabola in standard form, let's move on to finding the focus. The focus of a parabola can be found using the following formula:

p = 1 / (4a)

where p is the distance from the vertex to the focus, and a is the coefficient of the x^2 term in the standard form equation.

Step-by-Step Guide to Finding the Focus of a Parabola

Here's a step-by-step guide to finding the focus of a parabola in standard form:

1. Write down the equation of the parabola in standard form: y = ax^2 + bx + c
2. Identify the coefficient of the x^2 term (a)
3. Plug the value of a into the formula p = 1 / (4a)
4. Simplify the expression to find the value of p
5. The focus of the parabola is located at (h, k + p), where (h, k) is the vertex of the parabola

Examples of Finding the Focus of a Parabola

Let's work through a few examples to illustrate the process of finding the focus of a parabola in standard form.

Example 1: Find the Focus of the Parabola y = x^2 + 2x + 1

Using the formula p = 1 / (4a), we can find the value of p:

p = 1 / (4(1)) = 1/4

The focus of the parabola is located at (h, k + p), where (h, k) is the vertex of the parabola. Since the vertex is at (1, 1), the focus is located at (1, 1 + 1/4) = (1, 5/4).

Conclusion and Final Thoughts

In this article, we have explored how to find the focus of a parabola in standard form easily. By using the formula p = 1 / (4a) and following the step-by-step guide, you can find the focus of any parabola in standard form. Whether you're a student, teacher, or simply a math enthusiast, understanding how to find the focus of a parabola is a valuable skill that can help you tackle a wide range of problems in mathematics and real-world applications.

We hope this article has been helpful and informative. Do you have any questions or topics you'd like to discuss? Leave a comment below and let's get the conversation started!