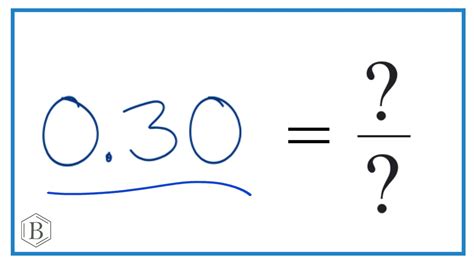30 As A Fraction Simplified

Quick Links :

Thirty is a whole number, and as a fraction, it can be represented in its simplest form as 30/1.

However, if you're looking for a fraction that equals 30, but with a different denominator, you can consider the following options:

• 60/2 = 30
• 90/3 = 30
• 120/4 = 30
• 150/5 = 30

In each of these cases, the numerator is a multiple of 30, and the denominator is a factor of that multiple.

It's worth noting that when simplifying a fraction, we aim to find the equivalent fraction with the smallest possible denominator. In this case, 30/1 is already in its simplest form, so there's no need for further simplification.

Understanding Fractions and Simplification

Fractions are a way of representing part of a whole as a ratio of two numbers. The top number, known as the numerator, tells us how many equal parts we have, while the bottom number, or denominator, tells us how many parts the whole is divided into.

Simplifying fractions is an essential math concept that helps us express fractions in their most basic form. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and denominator and divide both numbers by the GCD.

For example, let's simplify the fraction 12/16:

• Find the GCD of 12 and 16, which is 4.
• Divide both numbers by 4: 12 ÷ 4 = 3, and 16 ÷ 4 = 4.
• The simplified fraction is 3/4.

Why Simplify Fractions?

Simplifying fractions is crucial in various mathematical operations, such as adding, subtracting, multiplying, and dividing fractions. When fractions are in their simplest form, it's easier to perform these operations and compare fractions.

Moreover, simplifying fractions helps us:

• Identify equivalent fractions: By simplifying fractions, we can determine if two fractions are equivalent, even if they look different at first glance.
• Reduce errors: Simplifying fractions reduces the chance of errors in calculations, especially when working with complex fractions.
• Improve understanding: Simplifying fractions helps us understand the concept of fractions better and makes it easier to visualize the relationship between the numerator and denominator.

Real-World Applications of Fractions

Fractions are not just a math concept; they have numerous real-world applications in various fields, including:

• Cooking: Recipes often involve fractions, such as 1/4 cup or 3/4 teaspoon.
• Music: Music theory relies heavily on fractions to understand rhythm and timing.
• Finance: Fractions are used in interest rates, investment returns, and financial calculations.
• Science: Fractions are used to measure quantities, such as 3/4 of a liter or 2/3 of a kilogram.
• Engineering: Fractions are used in design, construction, and calculations involving proportions and ratios.

Common Fraction-Related Mistakes

When working with fractions, it's essential to avoid common mistakes, such as:

• Incorrectly adding or subtracting fractions with different denominators.
• Forgetting to simplify fractions before performing operations.
• Confusing equivalent fractions.

By understanding the basics of fractions, simplifying them correctly, and applying them to real-world scenarios, you'll become more confident in your math abilities and develop a stronger foundation for more advanced math concepts.

Conclusion and Next Steps

In conclusion, 30 as a fraction simplified is 30/1. However, understanding fractions and simplification is crucial for various mathematical operations and real-world applications.

To further develop your math skills, practice simplifying fractions and apply them to different scenarios. You can also explore more advanced math concepts, such as decimal and percentage conversions, or delve into algebra and geometry.

Remember to share your thoughts and questions in the comments below, and don't hesitate to ask for help when needed.