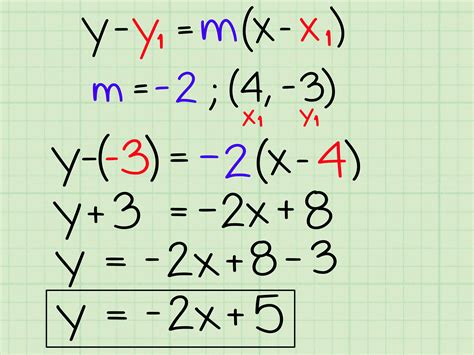Slope Intercept Form: Converting 4x + 8 To Y = Mx + B

Quick Links :

The slope-intercept form of a linear equation is a fundamental concept in algebra and is used to express the equation of a line in a way that makes it easy to identify the slope and the y-intercept. In this article, we will discuss the importance of the slope-intercept form, how to convert an equation from standard form to slope-intercept form, and provide practical examples and explanations.

The slope-intercept form of a linear equation is given by the equation y = mx + b, where m is the slope of the line and b is the y-intercept. The slope represents the rate at which the line rises or falls as you move from left to right, while the y-intercept is the point at which the line crosses the y-axis.

Converting an Equation from Standard Form to Slope-Intercept Form

The standard form of a linear equation is given by the equation Ax + By = C, where A, B, and C are constants. To convert an equation from standard form to slope-intercept form, we need to isolate the variable y. Let's take the equation 4x + 8 = 0 as an example.

First, we need to isolate the term with the variable y. Since there is no y variable in the equation, we can rearrange the equation to make y the subject.

Step 1: Rearrange the Equation

4x + 8 = 0

To isolate y, we can subtract 8 from both sides of the equation.

4x = -8

Next, we need to isolate the variable y by dividing both sides of the equation by the coefficient of x, which is 4.

Step 2: Isolate the Variable y

x = -8/4

x = -2

However, this equation is still not in slope-intercept form. To convert it to slope-intercept form, we need to express the equation in the form y = mx + b.

Step 3: Express the Equation in Slope-Intercept Form

Since the equation is already solved for x, we can rewrite it as:

y = -2x

Now, the equation is in slope-intercept form, with a slope of -2 and a y-intercept of 0.

Why is the Slope-Intercept Form Important?

The slope-intercept form is an important concept in algebra because it provides a way to easily identify the slope and the y-intercept of a line. This information can be used to graph the line, find the equation of a line given the slope and a point on the line, and solve systems of equations.

Identifying the Slope and Y-Intercept

When an equation is in slope-intercept form, the slope and the y-intercept can be easily identified. The slope is the coefficient of the variable x, and the y-intercept is the constant term.

For example, in the equation y = -2x + 3, the slope is -2 and the y-intercept is 3.

Applications of the Slope-Intercept Form

The slope-intercept form has many practical applications in fields such as physics, engineering, and economics. It can be used to model real-world phenomena, such as the motion of an object, the growth of a population, or the behavior of a financial market.

Example: Modeling the Motion of an Object

Suppose we want to model the motion of a car traveling at a constant speed of 60 miles per hour. We can use the slope-intercept form to express the equation of motion.

Let's assume that the car starts at a position of 0 miles and travels for a time t. The equation of motion can be expressed as:

s = 60t

where s is the position of the car and t is the time.

This equation is in slope-intercept form, with a slope of 60 and a y-intercept of 0.

Tips and Tricks for Converting Equations to Slope-Intercept Form

Converting an equation from standard form to slope-intercept form can be a challenging task, but with practice and patience, it can become easier. Here are some tips and tricks to help you convert equations to slope-intercept form:

Tip 1: Identify the Variable y

To convert an equation to slope-intercept form, you need to isolate the variable y. Make sure to identify the variable y and isolate it on one side of the equation.

Tip 2: Use the Inverse Operations

To isolate the variable y, you may need to use the inverse operations. For example, if you have an equation with a plus sign, you can use the inverse operation of subtraction to isolate the variable y.

Tip 3: Check Your Work

Once you have converted the equation to slope-intercept form, make sure to check your work. Plug in values for the variables and make sure that the equation is true.

Conclusion

In conclusion, the slope-intercept form is an important concept in algebra that provides a way to easily identify the slope and the y-intercept of a line. By following the steps outlined in this article, you can convert an equation from standard form to slope-intercept form. Remember to identify the variable y, use the inverse operations, and check your work to ensure that the equation is true.

We hope this article has been informative and helpful in understanding the concept of slope-intercept form. If you have any questions or comments, please feel free to leave them in the section below.