Fractions are a fundamental concept in mathematics, and simplifying them to their simplest form is an essential skill that can be applied in various mathematical operations. In this article, we will delve into the world of fractions, exploring the importance of simplifying them, the benefits of doing so, and providing a step-by-step guide on how to simplify fractions to their simplest form.
What are Fractions?

Fractions are a way to represent a part of a whole as a ratio of two numbers. The top number, known as the numerator, represents the number of equal parts, while the bottom number, known as the denominator, represents the total number of parts. For example, the fraction 3/4 represents three equal parts out of a total of four parts.
Why Simplify Fractions?

Simplifying fractions is crucial in mathematics because it helps to:
- Reduce errors: Simplifying fractions reduces the risk of errors when performing mathematical operations, such as addition, subtraction, multiplication, and division.
- Improve clarity: Simplified fractions are easier to read and understand, making it simpler to communicate mathematical ideas and solutions.
- Enhance problem-solving: Simplifying fractions can make it easier to identify equivalent ratios and proportions, which is essential in problem-solving.
Benefits of Simplifying Fractions
- Simplified fractions are easier to work with and can reduce calculation time.
- Simplifying fractions can help to identify equivalent ratios and proportions.
- Simplified fractions are more precise and accurate.
How to Simplify Fractions

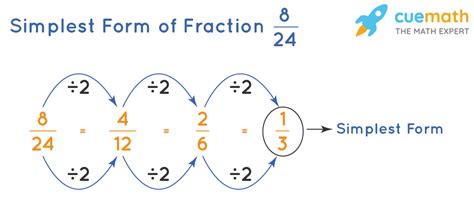
Simplifying fractions involves dividing both the numerator and the denominator by the greatest common divisor (GCD). Here's a step-by-step guide on how to simplify fractions:
- Find the GCD: Identify the greatest common divisor of the numerator and the denominator.
- Divide both numbers: Divide both the numerator and the denominator by the GCD.
- Check for further simplification: If the resulting fraction can be further simplified, repeat the process.
Example: Simplify the fraction 6/8.
- Find the GCD: The GCD of 6 and 8 is 2.
- Divide both numbers: Divide both 6 and 8 by 2.
- Check for further simplification: The resulting fraction 3/4 cannot be further simplified.
Simplifying Fractions with Variables
Simplifying fractions with variables involves factoring out common terms and canceling out like terms.
Example: Simplify the fraction (2x + 4)/(x + 2).
- Factor out common terms: Factor out 2 from the numerator and (x + 2) from the denominator.
- Cancel out like terms: Cancel out the common term (x + 2).
Result: The simplified fraction is 2.
Real-World Applications of Simplifying Fractions

Simplifying fractions has numerous real-world applications, including:
- Cooking and recipes: Simplifying fractions can help with scaling recipes and measuring ingredients accurately.
- Finance and economics: Simplifying fractions can help with calculating interest rates, investment returns, and financial ratios.
- Science and engineering: Simplifying fractions can help with calculating proportions, ratios, and quantities in scientific and engineering applications.
Common Mistakes to Avoid When Simplifying Fractions
- Dividing by zero: Avoid dividing both numbers by zero, as this can result in an undefined fraction.
- Not factoring out common terms: Failing to factor out common terms can result in an unsimplified fraction.
- Not canceling out like terms: Failing to cancel out like terms can result in an unsimplified fraction.
Conclusion

Simplifying fractions is a crucial skill in mathematics that can help reduce errors, improve clarity, and enhance problem-solving. By following the step-by-step guide outlined in this article, you can master the art of simplifying fractions and apply it to various mathematical operations and real-world applications.
Take the Next Step

Now that you've learned how to simplify fractions, it's time to put your skills to the test! Practice simplifying fractions with variables, and try applying the concept to real-world problems. Share your experiences and tips in the comments below, and don't forget to like and share this article with your friends and colleagues.
What is the purpose of simplifying fractions?
+Simplifying fractions reduces errors, improves clarity, and enhances problem-solving.
How do you simplify a fraction?
+Simplifying a fraction involves dividing both the numerator and the denominator by the greatest common divisor (GCD).
What are some common mistakes to avoid when simplifying fractions?
+Avoid dividing by zero, not factoring out common terms, and not canceling out like terms.