3 Easy Ways To Write Decimals Expanded Form

Quick Links :

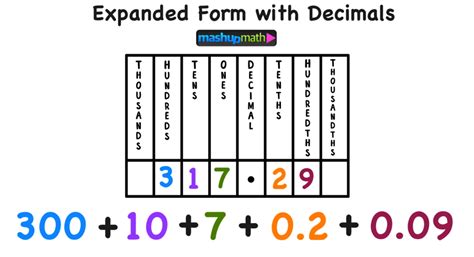
The world of decimals and expanded form - a crucial concept in mathematics that can seem daunting at first, but with the right approach, can become a breeze to master. Writing decimals in expanded form is an essential skill that helps students understand the place value of digits in a decimal number. In this article, we'll explore three easy ways to write decimals in expanded form, making it easier for you to grasp this concept.

Writing decimals in expanded form is a fundamental skill that not only helps students in mathematics but also in real-life applications, such as finance, science, and engineering. By breaking down a decimal number into its individual components, you can better understand the relationships between the digits and perform arithmetic operations with ease. So, let's dive into the three easy ways to write decimals in expanded form.

Method 1: The Digit-by-Digit Approach

The digit-by-digit approach involves breaking down a decimal number into its individual digits and then expressing each digit in terms of its place value. This method is straightforward and easy to understand, making it perfect for beginners.

Let's use the decimal number 4.27 as an example. To write this number in expanded form using the digit-by-digit approach, follow these steps:

• Identify the digits in the decimal number: 4, 2, and 7.
• Determine the place value of each digit: 4 is in the ones place, 2 is in the tenths place, and 7 is in the hundredths place.
• Express each digit in terms of its place value: 4 = 4 × 1, 2 = 2 × 0.1, and 7 = 7 × 0.01.
• Combine the expressions: 4 × 1 + 2 × 0.1 + 7 × 0.01.

The expanded form of 4.27 using the digit-by-digit approach is:

4 × 1 + 2 × 0.1 + 7 × 0.01

Example: Writing 3.14 in Expanded Form

Using the digit-by-digit approach, we can write 3.14 in expanded form as follows:

• Identify the digits: 3 and 1 and 4.
• Determine the place value: 3 is in the ones place, 1 is in the tenths place, and 4 is in the hundredths place.
• Express each digit in terms of its place value: 3 = 3 × 1, 1 = 1 × 0.1, and 4 = 4 × 0.01.
• Combine the expressions: 3 × 1 + 1 × 0.1 + 4 × 0.01.

The expanded form of 3.14 using the digit-by-digit approach is:

3 × 1 + 1 × 0.1 + 4 × 0.01

Method 2: The Block Method

The block method involves dividing a decimal number into blocks of digits, with each block representing a specific place value. This method is useful for larger decimal numbers and helps to organize the digits in a more visual way.

Let's use the decimal number 12.345 as an example. To write this number in expanded form using the block method, follow these steps:

• Divide the decimal number into blocks: 12, 3, 4, and 5.
• Determine the place value of each block: 12 is in the ones and tenths place, 3 is in the hundredths place, 4 is in the thousandths place, and 5 is in the ten-thousandths place.
• Express each block in terms of its place value: 12 = 12 × 1, 3 = 3 × 0.01, 4 = 4 × 0.001, and 5 = 5 × 0.0001.
• Combine the expressions: 12 × 1 + 3 × 0.01 + 4 × 0.001 + 5 × 0.0001.

The expanded form of 12.345 using the block method is:

12 × 1 + 3 × 0.01 + 4 × 0.001 + 5 × 0.0001

Example: Writing 6.789 in Expanded Form

Using the block method, we can write 6.789 in expanded form as follows:

• Divide the decimal number into blocks: 6, 7, 8, and 9.
• Determine the place value of each block: 6 is in the ones place, 7 is in the tenths place, 8 is in the hundredths place, and 9 is in the thousandths place.
• Express each block in terms of its place value: 6 = 6 × 1, 7 = 7 × 0.1, 8 = 8 × 0.01, and 9 = 9 × 0.001.
• Combine the expressions: 6 × 1 + 7 × 0.1 + 8 × 0.01 + 9 × 0.001.

The expanded form of 6.789 using the block method is:

6 × 1 + 7 × 0.1 + 8 × 0.01 + 9 × 0.001

Method 3: The Decimal Fraction Method

The decimal fraction method involves converting a decimal number to a fraction and then expressing it in expanded form. This method is useful for smaller decimal numbers and helps to develop a deeper understanding of fractions.

Let's use the decimal number 0.5 as an example. To write this number in expanded form using the decimal fraction method, follow these steps:

• Convert the decimal number to a fraction: 0.5 = 5/10.
• Simplify the fraction: 5/10 = 1/2.
• Express the fraction in expanded form: 1/2 = 1 × 0.5.

The expanded form of 0.5 using the decimal fraction method is:

1 × 0.5

Example: Writing 0.25 in Expanded Form

Using the decimal fraction method, we can write 0.25 in expanded form as follows:

• Convert the decimal number to a fraction: 0.25 = 25/100.
• Simplify the fraction: 25/100 = 1/4.
• Express the fraction in expanded form: 1/4 = 1 × 0.25.

The expanded form of 0.25 using the decimal fraction method is:

1 × 0.25

As you can see, each method has its unique approach to writing decimals in expanded form. By mastering these methods, you'll be able to tackle even the most complex decimal numbers with ease.

Now, we'd like to hear from you! Which method do you think is the most effective for writing decimals in expanded form? Do you have any questions or need further clarification on any of the methods? Please leave a comment below and let's get the conversation started.