Write The Equation Of A Line In Slope-Intercept Form

Quick Links :

The Equation of a Line in Slope-Intercept Form

Lines are a fundamental concept in mathematics, and understanding how to represent them in different forms is crucial for problem-solving and analytical thinking. The slope-intercept form is one of the most widely used forms to represent a linear equation. It provides a straightforward way to identify the slope and the y-intercept of a line.

In this article, we will delve into the world of slope-intercept form, exploring its definition, benefits, and applications. We will also learn how to convert a linear equation from other forms to slope-intercept form and vice versa.

What is Slope-Intercept Form?

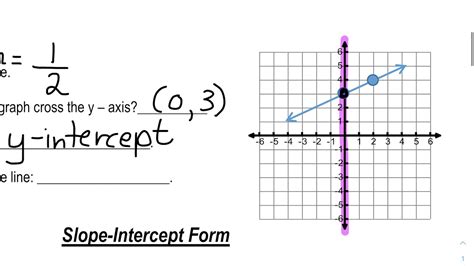
The slope-intercept form of a linear equation is represented by the formula y = mx + b, where:

• m is the slope of the line, which measures how steep it is.
• b is the y-intercept, which is the point where the line crosses the y-axis.

In this form, the slope (m) represents the rate of change of the line, while the y-intercept (b) indicates the starting point of the line on the y-axis.

Benefits of Slope-Intercept Form

The slope-intercept form offers several benefits that make it a popular choice among mathematicians and scientists:

• Easy to identify slope and y-intercept: The slope-intercept form makes it straightforward to determine the slope and y-intercept of a line, which is essential for understanding its behavior.
• Simple to graph: With the slope and y-intercept, graphing a line becomes a breeze. Simply plot the y-intercept and use the slope to draw the line.
• Convenient for solving systems of equations: Slope-intercept form makes it easy to solve systems of linear equations by substitution or elimination.

How to Convert to Slope-Intercept Form

Converting a linear equation from another form to slope-intercept form is a straightforward process. Here's a step-by-step guide:

1. Start with a linear equation in any form (e.g., standard form, point-slope form).
2. Rearrange the equation to isolate y on one side of the equation.
3. Simplify the equation to obtain the slope-intercept form (y = mx + b).

For example, let's convert the equation 2x + 3y = 6 to slope-intercept form:

1. Rearrange the equation to isolate y: 3y = -2x + 6
2. Simplify the equation: y = (-2/3)x + 2

The resulting equation is in slope-intercept form, where m = -2/3 and b = 2.

Real-World Applications of Slope-Intercept Form

Slope-intercept form has numerous real-world applications across various fields:

• Physics and engineering: The slope-intercept form is used to describe the motion of objects, model population growth, and optimize systems.
• Economics: Slope-intercept form is used to analyze the relationship between economic variables, such as supply and demand.
• Computer science: The slope-intercept form is used in computer graphics, game development, and machine learning.

Common Mistakes to Avoid

When working with slope-intercept form, be mindful of the following common mistakes:

• Incorrectly identifying the slope and y-intercept: Double-check that you have correctly identified the slope and y-intercept from the equation.
• Failing to simplify the equation: Make sure to simplify the equation to obtain the slope-intercept form.

Conclusion and Call to Action

In conclusion, the slope-intercept form is a fundamental concept in mathematics that provides a straightforward way to represent linear equations. By understanding the benefits, applications, and how to convert to slope-intercept form, you'll become more proficient in solving linear equations and modeling real-world problems.

Take the next step by practicing converting linear equations to slope-intercept form and exploring its applications in various fields. Share your experiences and questions in the comments below!