Graphing Quadratics From Standard Form Worksheet & Answers

Quick Links :

Graphing quadratics is a fundamental concept in algebra, and understanding how to graph them from standard form is crucial for students to succeed in mathematics. In this article, we will delve into the world of quadratic equations, explore the standard form, and provide a comprehensive guide on how to graph quadratics from standard form.

Understanding Quadratic Equations

Quadratic equations are polynomial equations of degree two, which means the highest power of the variable (usually x) is two. A quadratic equation can be written in the general form of ax^2 + bx + c = 0, where a, b, and c are constants, and a cannot be equal to zero.

Standard Form of a Quadratic Equation

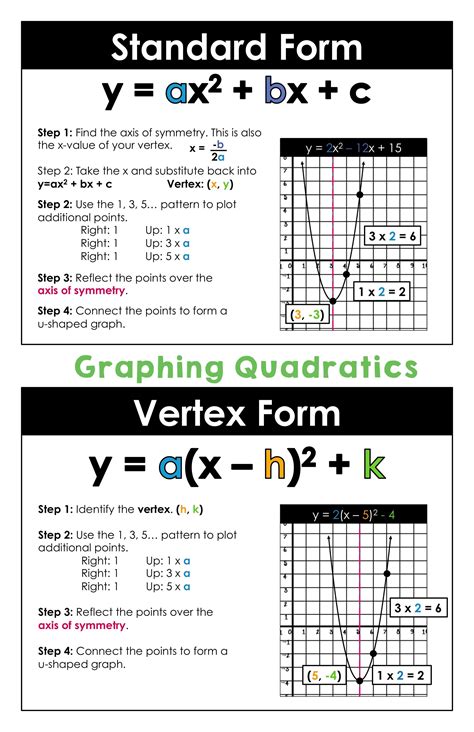
The standard form of a quadratic equation is f(x) = ax^2 + bx + c, where a, b, and c are constants. This form is useful for graphing quadratics, as it allows us to identify the vertex, axis of symmetry, and x-intercepts of the parabola.

Graphing Quadratics from Standard Form

Graphing quadratics from standard form involves several steps:

1. Identify the vertex of the parabola using the formula x = -b/2a.
2. Determine the axis of symmetry, which is the vertical line that passes through the vertex.
3. Find the x-intercepts of the parabola by setting f(x) = 0 and solving for x.
4. Determine the direction of the parabola (opens up or down) based on the value of a.
5. Plot the vertex, axis of symmetry, and x-intercepts on the graph.
6. Connect the points with a smooth curve to form the parabola.

Example 1: Graphing a Quadratic from Standard Form

Consider the quadratic equation f(x) = x^2 + 4x + 4. To graph this equation, we need to follow the steps outlined above.

• Identify the vertex: x = -b/2a = -4/(2*1) = -2
• Determine the axis of symmetry: x = -2
• Find the x-intercepts: f(x) = x^2 + 4x + 4 = 0 => x = -2
• Determine the direction: a = 1 > 0, so the parabola opens up
• Plot the vertex, axis of symmetry, and x-intercepts: (-2, 0)
• Connect the points with a smooth curve to form the parabola.

Benefits of Graphing Quadratics from Standard Form

Graphing quadratics from standard form has several benefits:

• It allows students to visualize the relationship between the quadratic equation and its graph.
• It helps students understand the properties of the parabola, such as the vertex, axis of symmetry, and x-intercepts.
• It enables students to identify the direction of the parabola and determine whether it opens up or down.
• It provides a foundation for more advanced math concepts, such as quadratic functions and systems of equations.

Common Challenges and Solutions

Graphing quadratics from standard form can be challenging, especially for students who are new to algebra. Here are some common challenges and solutions:

• Challenge: Identifying the vertex and axis of symmetry.
• Solution: Use the formula x = -b/2a to find the vertex, and then determine the axis of symmetry.
• Challenge: Finding the x-intercepts.
• Solution: Set f(x) = 0 and solve for x using factoring, quadratic formula, or other methods.
• Challenge: Determining the direction of the parabola.
• Solution: Check the value of a. If a > 0, the parabola opens up. If a < 0, the parabola opens down.

Practice Worksheet

Here is a practice worksheet to help you reinforce your understanding of graphing quadratics from standard form:

1. Graph the quadratic equation f(x) = x^2 + 2x + 1.
2. Graph the quadratic equation f(x) = x^2 - 4x - 3.
3. Graph the quadratic equation f(x) = 2x^2 + 5x + 3.

Answers to Practice Worksheet

1. The graph of f(x) = x^2 + 2x + 1 is a parabola that opens up with vertex (-1, 0) and axis of symmetry x = -1.
2. The graph of f(x) = x^2 - 4x - 3 is a parabola that opens up with vertex (2, -7) and axis of symmetry x = 2.
3. The graph of f(x) = 2x^2 + 5x + 3 is a parabola that opens up with vertex (-5/4, -25/8) and axis of symmetry x = -5/4.

Conclusion

Graphing quadratics from standard form is an essential skill in algebra, and it requires a deep understanding of the quadratic equation and its properties. By following the steps outlined in this article, you can become proficient in graphing quadratics from standard form and develop a strong foundation for more advanced math concepts.

We hope this article has been informative and helpful in your understanding of graphing quadratics from standard form. If you have any questions or need further clarification, please don't hesitate to ask.