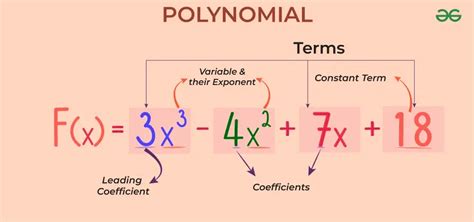
Polynomials In Standard Form: A Simple Explanation

Quick Links :

Polynomials are a fundamental concept in algebra, and understanding their standard form is crucial for working with them effectively. In this article, we will delve into the world of polynomials, exploring what they are, why they are important, and how to express them in standard form.

Mathematics is the language of problem-solving, and polynomials are a key part of that language. They are used to describe a wide range of phenomena, from the growth of populations to the movement of objects in physics. In essence, polynomials are expressions consisting of variables and coefficients combined using only addition, subtraction, and multiplication.

One of the most important aspects of polynomials is their ability to be expressed in standard form. This form makes it easy to identify the degree of the polynomial, as well as the coefficients of each term. In this article, we will explore the benefits of expressing polynomials in standard form and provide a step-by-step guide on how to do it.

What is Standard Form?

Standard form is a way of writing polynomials that makes it easy to compare and contrast different expressions. It involves arranging the terms of the polynomial in descending order of their degrees. This means that the term with the highest degree comes first, followed by the term with the next highest degree, and so on.

For example, consider the polynomial 3x^2 + 2x - 4. In standard form, this polynomial would be written as 3x^2 + 2x - 4. Notice that the term with the highest degree (x^2) comes first, followed by the term with the next highest degree (x), and finally the constant term (-4).

Benefits of Standard Form

Expressing polynomials in standard form has several benefits. For one, it makes it easy to identify the degree of the polynomial, which is important for determining the number of solutions it has. Additionally, standard form makes it easy to compare and contrast different polynomials, which is important for solving equations and inequalities.

Furthermore, standard form is useful for adding and subtracting polynomials. When polynomials are in standard form, it is easy to combine like terms and simplify the expression.

How to Express Polynomials in Standard Form

Expressing polynomials in standard form is a simple process that involves arranging the terms in descending order of their degrees. Here are the steps:

1. Write down the polynomial expression.
2. Identify the degree of each term.
3. Arrange the terms in descending order of their degrees.
4. Combine like terms.

For example, consider the polynomial 2x + 3x^2 - 4. To express this polynomial in standard form, we would follow these steps:

1. Write down the polynomial expression: 2x + 3x^2 - 4
2. Identify the degree of each term: 2x (degree 1), 3x^2 (degree 2), -4 (degree 0)
3. Arrange the terms in descending order of their degrees: 3x^2 + 2x - 4
4. Combine like terms: none in this case

Common Mistakes to Avoid

When expressing polynomials in standard form, there are several common mistakes to avoid. One of the most common mistakes is to forget to combine like terms. This can result in a polynomial that is not in standard form.

Another common mistake is to arrange the terms in ascending order of their degrees, rather than descending order. This can also result in a polynomial that is not in standard form.

Practical Applications of Polynomials in Standard Form

Polynomials in standard form have many practical applications in mathematics, science, and engineering. They are used to model real-world phenomena, such as population growth and motion of objects.

For example, consider a company that produces and sells a product. The company's profit can be modeled using a polynomial expression. By expressing this polynomial in standard form, the company can easily identify the degree of the polynomial and make predictions about future profits.

Real-World Examples

Here are some real-world examples of polynomials in standard form:

• The profit of a company can be modeled using the polynomial expression 2x^2 + 3x - 4, where x is the number of units produced and sold.
• The motion of an object can be modeled using the polynomial expression x^2 + 2x + 1, where x is the time and the coefficients represent the acceleration and velocity of the object.
• The growth of a population can be modeled using the polynomial expression 3x^2 + 2x - 1, where x is the time and the coefficients represent the birth and death rates.

Conclusion: A Simple Yet Powerful Tool

Expressing polynomials in standard form is a simple yet powerful tool that has many practical applications in mathematics, science, and engineering. By understanding how to express polynomials in standard form, we can easily identify the degree of the polynomial, combine like terms, and make predictions about future outcomes.

Whether you are a student, teacher, or professional, understanding polynomials in standard form is essential for working with mathematical expressions effectively. With this knowledge, you can unlock the secrets of polynomials and apply them to real-world problems.

Now that you have learned about polynomials in standard form, we encourage you to share your thoughts and comments below. How do you use polynomials in your daily life? Do you have any tips or tricks for working with polynomials? Share your experiences and help others learn from your expertise.