Planes Intersect Forming A Line

Quick Links :

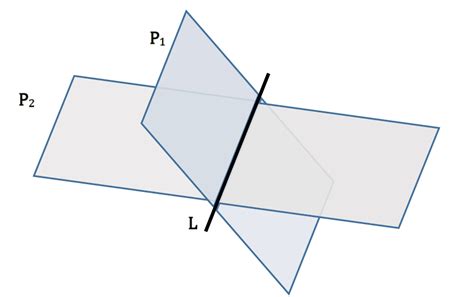
When two planes intersect, they form a line. This concept is fundamental in geometry and is used in various mathematical and real-world applications. The intersection of two planes is a crucial concept in understanding the relationships between planes and their spatial configurations. In this article, we will delve into the concept of planes intersecting to form a line, exploring the mathematical and practical aspects of this phenomenon.

Mathematical Representation

In mathematics, a plane is represented by an equation in the form ax + by + cz + d = 0, where a, b, c, and d are constants. When two planes intersect, their equations are satisfied simultaneously, resulting in a system of linear equations. By solving this system, we can determine the equation of the line formed by the intersection of the two planes.

For example, consider two planes with equations:

2x + 3y - z + 1 = 0 x - 2y + 4z - 3 = 0

To find the intersection line, we need to solve the system of equations:

2x + 3y - z + 1 = 0 x - 2y + 4z - 3 = 0

By solving this system, we can obtain the equation of the line formed by the intersection of the two planes.

Parametric and Symmetric Forms

The equation of the line formed by the intersection of two planes can be represented in parametric or symmetric form. The parametric form represents the line in terms of a parameter, usually t, while the symmetric form represents the line in terms of the coordinates x, y, and z.

For instance, the parametric form of the line formed by the intersection of the two planes above can be represented as:

x = 2t + 1 y = -t + 2 z = 3t - 1

On the other hand, the symmetric form of the line can be represented as:

x = 2y - z + 1 y = -x + 4z - 3 z = -2x + 3y + 1

Geometric Interpretation

Geometrically, the intersection of two planes forms a line that lies on both planes. This line is called the common line or the intersection line of the two planes. The direction of the line is perpendicular to the normal vectors of both planes.

In three-dimensional space, the intersection line of two planes can be visualized as a line that passes through the point of intersection of the two planes. The line is perpendicular to both planes and can be represented by a vector that is perpendicular to both normal vectors of the planes.

Applications in Computer Graphics and Engineering

The concept of planes intersecting to form a line has numerous applications in computer graphics and engineering. In computer-aided design (CAD) software, the intersection of planes is used to create complex shapes and models. In engineering, the intersection of planes is used to determine the stresses and loads on structures, such as bridges and buildings.

For instance, in computer graphics, the intersection of planes is used to render 3D scenes and simulate realistic lighting effects. In engineering, the intersection of planes is used to analyze the structural integrity of buildings and bridges, ensuring that they can withstand external loads and stresses.

Special Cases and Exceptions

There are special cases and exceptions when two planes intersect. For instance, if the two planes are parallel, they do not intersect, and there is no common line. If the two planes are identical, they intersect at every point on the plane, and there is no unique common line.

In some cases, the intersection line of two planes may be undefined or infinite. For example, if the two planes are parallel and do not intersect, the intersection line is undefined. If the two planes are identical, the intersection line is infinite, as every point on the plane is a point of intersection.

Conclusion and Future Directions

In conclusion, the intersection of two planes forms a line that lies on both planes. The equation of the line can be represented in parametric or symmetric form, and the direction of the line is perpendicular to the normal vectors of both planes. The concept of planes intersecting to form a line has numerous applications in computer graphics and engineering, and is a fundamental concept in understanding the relationships between planes and their spatial configurations.

Future research directions may include exploring the intersection of multiple planes and the formation of complex shapes and structures. Additionally, the application of the concept of planes intersecting to form a line in fields such as robotics and artificial intelligence may lead to innovative solutions and advancements.