What Is A Quadratic Equation In Standard Form

Quick Links :

Quadratic equations are a fundamental concept in algebra and are used to describe a wide range of phenomena in mathematics, physics, engineering, and other fields. A quadratic equation in standard form is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two.

Understanding Quadratic Equations

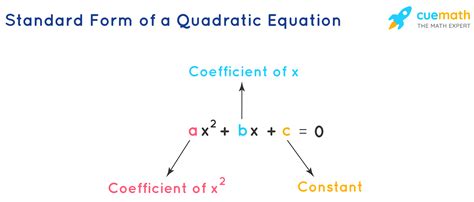
A quadratic equation in standard form is written as:

ax^2 + bx + c = 0

where:

• a is the coefficient of the x^2 term (also known as the quadratic coefficient)
• b is the coefficient of the x term (also known as the linear coefficient)
• c is the constant term
• x is the variable

For example, the following equation is a quadratic equation in standard form:

x^2 + 4x + 4 = 0

In this equation, a = 1, b = 4, and c = 4.

Key Features of Quadratic Equations

Quadratic equations have several key features that are important to understand:

• The highest power of the variable is two, which means the graph of the equation will be a parabola.
• The equation can be factored, which means it can be written as a product of two binomials.
• The equation can have zero, one, or two real solutions.
• The equation can be solved using various methods, including factoring, the quadratic formula, and graphing.

Working with Quadratic Equations

There are several ways to work with quadratic equations, including:

• Factoring: This involves expressing the equation as a product of two binomials.
• Quadratic Formula: This involves using a formula to find the solutions of the equation.
• Graphing: This involves graphing the equation on a coordinate plane to visualize the solutions.

Factoring Quadratic Equations

Factoring quadratic equations involves expressing the equation as a product of two binomials. For example, the equation:

x^2 + 4x + 4 = 0

can be factored as:

(x + 2)(x + 2) = 0

This tells us that the solutions to the equation are x = -2.

Using the Quadratic Formula

The quadratic formula is a formula that can be used to find the solutions of a quadratic equation. The formula is:

x = (-b ± √(b^2 - 4ac)) / 2a

This formula can be used to find the solutions of any quadratic equation.

Applications of Quadratic Equations

Quadratic equations have a wide range of applications in mathematics, physics, engineering, and other fields. Some examples include:

• Projectile motion: Quadratic equations can be used to model the trajectory of a projectile under the influence of gravity.
• Electrical circuits: Quadratic equations can be used to model the behavior of electrical circuits.
• Population growth: Quadratic equations can be used to model the growth of populations.

Real-World Examples

Quadratic equations are used in a wide range of real-world applications, including:

• Designing roller coasters: Quadratic equations can be used to model the shape of a roller coaster track.
• Predicting stock prices: Quadratic equations can be used to model the behavior of stock prices.
• Optimizing resources: Quadratic equations can be used to optimize the use of resources in a variety of applications.

Conclusion and Future Directions

In conclusion, quadratic equations are a fundamental concept in algebra and are used to describe a wide range of phenomena in mathematics, physics, engineering, and other fields. Understanding quadratic equations and how to work with them is essential for anyone interested in pursuing a career in these fields.

We hope this article has provided a comprehensive overview of quadratic equations and their applications. We encourage you to share your thoughts and comments on the topic and to continue exploring the world of quadratic equations.