What Is A Polynomial In Standard Form

Quick Links :

Polynomials are a fundamental concept in algebra, and understanding their standard form is crucial for working with them effectively. In this article, we will delve into the world of polynomials, exploring what they are, their importance, and how to express them in standard form.

Polynomials are mathematical expressions consisting of variables and coefficients combined using only addition, subtraction, and multiplication. They are used to model a wide range of real-world phenomena, from the growth of populations to the motion of objects. Polynomials are essential in various fields, including physics, engineering, economics, and computer science.

The standard form of a polynomial is a way of writing it in a specific format, making it easier to work with and understand. It is a crucial concept in algebra, as it allows us to perform operations such as addition, subtraction, and multiplication on polynomials.

What is a Polynomial?

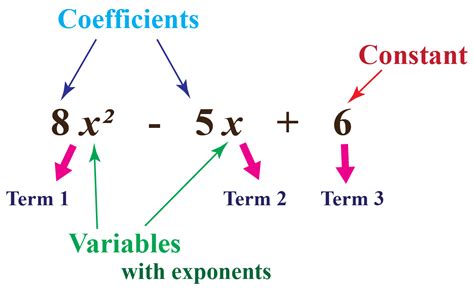
A polynomial is an expression consisting of variables and coefficients combined using only addition, subtraction, and multiplication. The variables in a polynomial are typically represented by letters such as x, y, or z, while the coefficients are numerical constants. For example:

2x^2 + 3x - 4

In this example, 2x^2, 3x, and -4 are the terms of the polynomial. The variables are x, and the coefficients are 2, 3, and -4.

Importance of Polynomials

Polynomials are used to model a wide range of real-world phenomena, making them essential in various fields. Some of the importance of polynomials includes:

• Modeling population growth: Polynomials can be used to model the growth of populations, helping us understand how populations change over time.
• Describing motion: Polynomials can be used to describe the motion of objects, including the position, velocity, and acceleration of an object.
• Analyzing data: Polynomials can be used to analyze data, helping us understand patterns and trends in data.
• Solving equations: Polynomials can be used to solve equations, which is essential in various fields such as physics, engineering, and economics.

What is Standard Form?

The standard form of a polynomial is a way of writing it in a specific format, making it easier to work with and understand. In standard form, the terms of the polynomial are written in descending order of the exponent of the variable. For example:

x^2 + 3x - 4

This is the standard form of the polynomial 2x^2 + 3x - 4. The terms are written in descending order of the exponent of the variable x.

How to Write a Polynomial in Standard Form

Writing a polynomial in standard form is a straightforward process. Here are the steps:

1. Write the terms of the polynomial in descending order of the exponent of the variable.
2. Combine like terms, which are terms with the same exponent.
3. Simplify the polynomial by combining any constant terms.

For example:

2x^2 + 3x + x^2 - 4

To write this polynomial in standard form, we need to follow the steps:

1. Write the terms in descending order of the exponent: 2x^2 + x^2 + 3x - 4
2. Combine like terms: 3x^2 + 3x - 4
3. Simplify the polynomial: 3x^2 + 3x - 4

The resulting polynomial is in standard form.

Examples of Polynomials in Standard Form

Here are some examples of polynomials in standard form:

• x^2 + 2x - 3
• 2x^3 - 5x^2 + x - 1
• x^4 - 2x^3 + 3x^2 - 4x + 1

These polynomials are all in standard form, with the terms written in descending order of the exponent of the variable.

Benefits of Writing Polynomials in Standard Form

Writing polynomials in standard form has several benefits, including:

• Easier to work with: Polynomials in standard form are easier to add, subtract, and multiply.
• Easier to understand: Polynomials in standard form are easier to understand, as the terms are written in a specific format.
• Simplifies calculations: Writing polynomials in standard form simplifies calculations, as like terms can be combined.

In conclusion, understanding what a polynomial is and how to write it in standard form is crucial in algebra. Polynomials are used to model a wide range of real-world phenomena, and writing them in standard form makes it easier to work with and understand them. By following the steps outlined in this article, you can write polynomials in standard form and take advantage of the benefits it provides.